Eine wesentliche Aufgabe des Mathematikunterrichts in der Grundschule stellt die Entwicklung eines tragfähigen Zahlverständnisses dar. Demnach sollen Kinder Zahlen nicht nur als Zahlsymbole wahrnehmen, sondern umfangreiche Vorstellungen zu diesen aufbauen, die sie im Laufe der Zeit flexibel abrufen können.
-
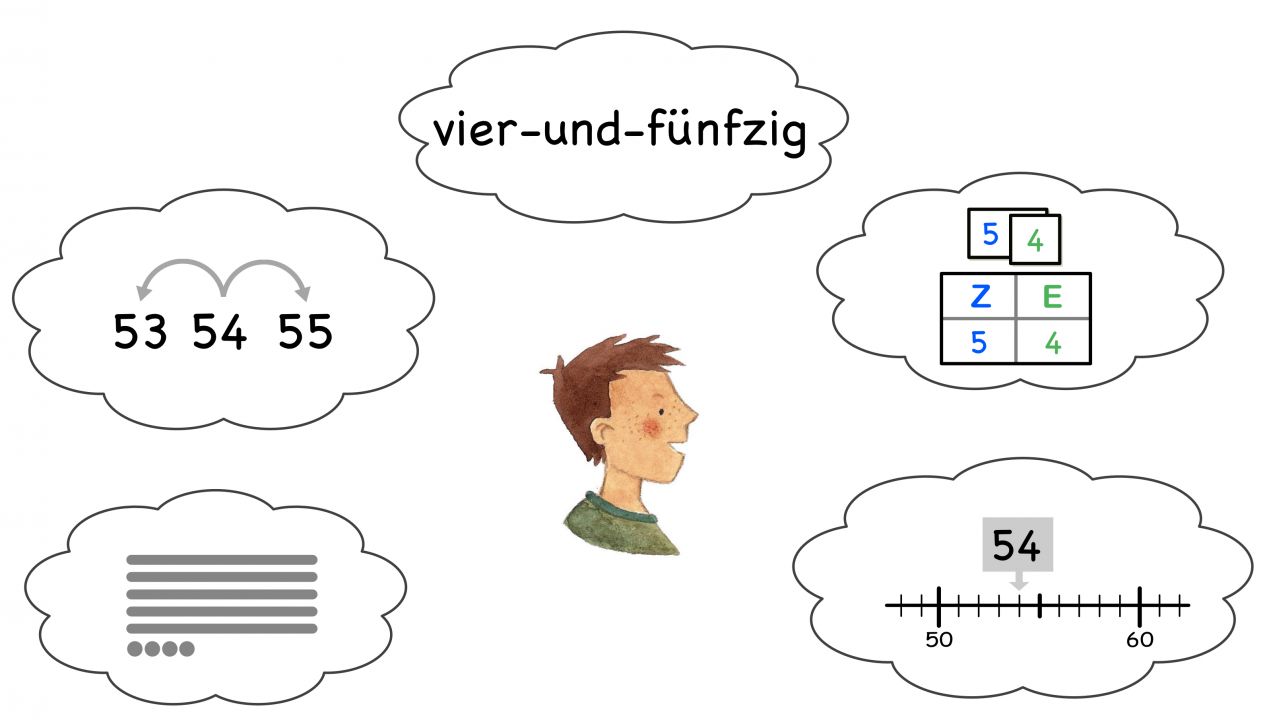
Wie heißt die Zahl? Wie sieht sie aus? Wie lässt sie sich unterschiedlich darstellen?
-
Wo befindet sie sich in der Zahlenreihe? Welche Nachbarzahlen hat sie?
-
In welcher Beziehung steht die Zahl zu anderen Zahlen?
-
In welche Zahlen lässt sich die Zahl zerlegen?
Die Entwicklung eines tragfähigen Zahlverständnisses sowie die Einsicht in Zahlbeziehungen und unser Stellenwertsystem beginnen bereits grundlegend im Anfangsunterricht, so dass die Vorstellungen bei der Erweiterung des Zahlenraums aufgegriffen und strukturgleich weiterentwickelt werden. Folglich ist ein frühzeitiger Aufbau des Zahlverständnisses bedeutsam für die Prävention von Matheschwierigkeiten. Bereits im Anfangsunterricht sollten daher die individuellen Vorkenntnisse der Kinder im Zahlenraum bis 10 bzw. bis 20 berücksichtigt werden, um durch geeignete Förderanregungen das Zahlverständnis ausweiten zu können. Um jedoch Zahlen mit vielfältigen Bedeutungen verknüpfen zu können, muss der Unterricht ausreichend Gelegenheiten bieten, ein umfangreiches Zahlverständnis zu entwickeln. Für die Unterrichtsgestaltung bedeutet dies, ähnlich zur Förderung des Operationsverständnisses, dass Kinder:

Grundvorstellungen entwickeln
Wesentlich für den Erwerb tragfähiger Grundvorstellungen sind insbesondere der Aufbau und die Festigung des kardinalen und ordinalen Zahlverständnisses sowie des Stellenwertverständnisses.
Der kardinale Zahlaspekt beschreibt die Erfassung von Zahlen als Anzahlen von Objekten einer Menge. Durch die Verwendung strukturierter Darstellungen (z. B. Zwanzigerfeld) können die Lernenden die Anzahlen der Objekte nicht nur durch reines Auszählen, sondern auch quasi-simultan mit Hilfe der Fünfer- und Zehner-Struktur ermitteln.

Der ordinale Zahlaspekt beschreibt die Folge der natürlichen Zahlen und entsprechende lineare Darstellungen (z. B. Zwanzigerkette, Zahlenstrahl). Jedem Objekt wird beim Zählen genau ein Zahlwort zugeordnet, wodurch Rangplätze ermittelt werden können. Voraussetzung hierfür ist die gesicherte Kenntnis der Zahlwortreihe (Selter & Zannetin, 2018; Krauthausen, 2018; Schipper, 2009).

Darstellungen vernetzen
Die Fähigkeit zum Darstellungswechsel ist wesentlich für die flexible Nutzung der unterschiedlichen Darstellungsformen von Zahlen:
Handlungen mit Material, Bilder, gesprochene oder geschriebene Sprache und symbolische Darstellungen (Mathesprache). Für den Aufbau und die Festigung von Zahlvorstellungen im Anfangsunterricht sind bildliche Darstellungen und Handlungen mit Material von besonderer Bedeutung, da sie an die Alltagserfahrungen der Kinder anknüpfen und diese aufgreifen. Durch die Vernetzung der Darstellungsformen kann eine Verständnisgrundlage für die Nutzung der mathematischen Symbole geschaffen werden, weshalb alle Darstellungsformen im Lernprozess immer wieder zum Tragen kommen sollen (Kuhnke, 2012).

Zahlbeziehungen nutzen
Die Nutzung von Zahlbeziehungen ist eine zenztrale Voraussetzung für die Entwicklung und Nutzung flexibler Rechenstrategien, denn jede Zahl steht als Vorgänger, Nachfolger oder Vielfaches in Beziehung zu anderen Zahlen und kann zerlegt werden. Diese Teil-Teil-Ganzes-Beziehungen gilt es in einem verständnisbasierten Mathematikunterricht herauszuarbeiten und für flexible mentale Zahlvorstellungen sowie zur Nutzung flexibler Rechenstrategien nutzbar zu machen (Gerster & Schultz, 2004; Gaidoschik, 2010).
Weiterführende Informationen zum Aufbau eines tragfähigen Zahlverständnisses finden Sie auch im nachfolgenden Video des Projekts DigiMal.nrw:
Hintergrundwissen und Material in den Partnerprojekten
Weiterführenden Informationen zur Vertiefung sowie Material zum Einsatz im Unterricht finden Sie auch auf folgenden Partnerprojektseiten:
Mathe inklusiv
Hintergrundinformationen und Unterrichtsmaterialien zum Aufbau von Zahlvorstellungen im inklusiven Mathematikunterricht.
primakom
Hintergrundwissen und Unterrichtsmaterialien zum Aufbau eines tragfähigen Zahlverständnisses.
Mathe sicher können (Förderbausteine N02 und N2)
Förderung des Zahlverständnisses mit Hilfe von Diagnose- und Fördermaterial zum Ordnen und Vergleichen von Zahlen.
KIRA
Hintergrundinformationen und Kinderdokumente zum Aufbau eines tragfähigen Zahlverständnisses.
Mahiko ZR bis 20 und ZR bis 100
Grundlagenwissen zum Aufbau eines tragfähigen Zahlverständnisses in den Modulen "Zählen", "Zahlen darstellen", "Zahlen schnell sehen", "Zahlen vergleichen und ordnen" und "Zahlen zerlegen"