Während es bei der Entwicklung des Zahlverständnisses darum geht, die Bedeutung der Zahlen zu verstehen, Zahlen zu vergleichen und zu zerlegen sowie Zahlen in Beziehung zueinander zu erkennen, liegt bei der Entwicklung des Operationsverständnisses der Fokus darauf, die vier Grundrechenoperationen zu verstehen und diese mit Bedeutungen zu verknüpfen. Dies soll nachfolgend am Beispiel der Multiplikation veranschaulicht werden.
-
Was bedeutet eigentlich multiplizieren?
-
Welche Handlungen können sich hinter dem Malzeichen verbergen?
-
Was passiert mit den Zahlen, wenn man sie multipliziert?
Um ein tragfähiges Operationsverständnis zu entwickeln und dieses flexibel abrufen zu können, sollen Lernende im Unterricht ausreichend Gelegenheiten bekommen, Vorstellungsbilder (materialgestützt) aufzubauen. Am Beispiel der Multiplikation zeigt die Grafik, wie die Schülerin die formale Malaufgabe mit (Handlungs-)Erfahrungen verknüpft.
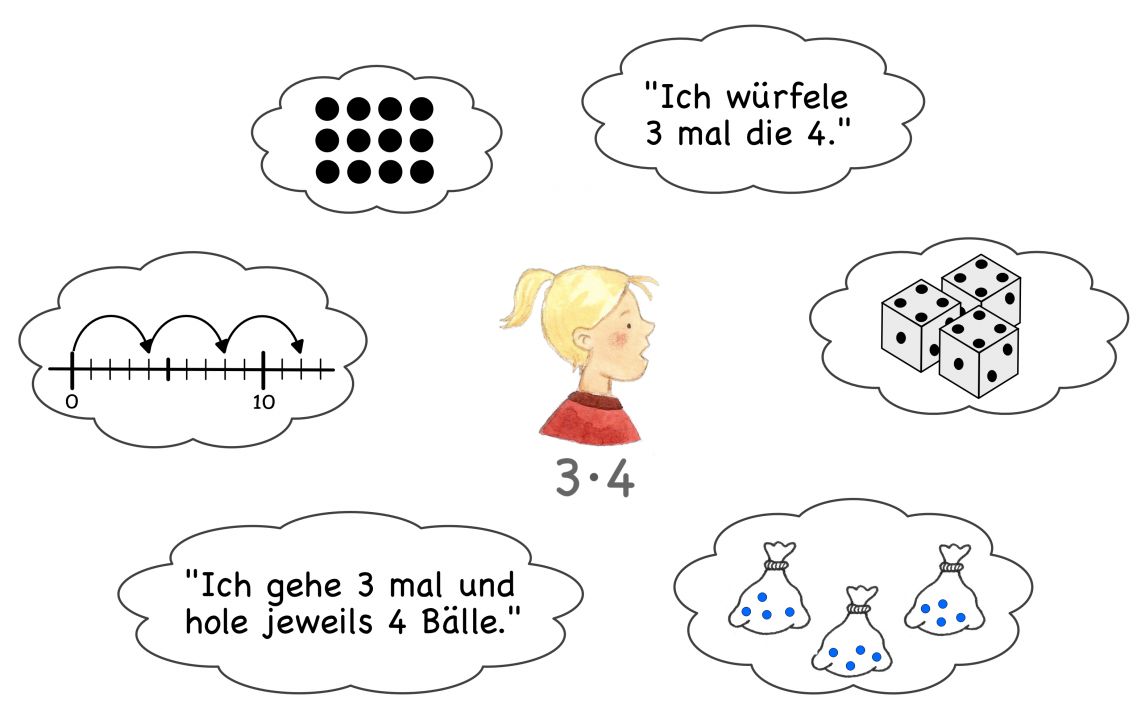
Die Kinder bauen so im Laufe der Zeit ein Repertoire an Vorstellungsbildern auf, welches es ihnen ermöglicht, multiplikative Strukturen in unterschiedlichen Situationen und in verschiedenen Darstellungsformen zu erkennen und auf andere Situationen zu übertragen.
Zentral ist, dass Kinder ausreichend Gelegenheiten bekommen, diese Vorstellungen zu entwickeln. Folgende drei Aspekte sollten daher bei der Unterrichtsplanung, analog zum Aufbau des Zahlverständnisses, Berücksichtigung finden:

Grundvorstellungen entwickeln
Damit Kinder nicht nur die formalen Rechenzeichen sehen, sondern die Bedeutung hinter der Rechenoperation verstehen und begründet entscheiden können, wann sie minus, plus, mal oder geteilt rechnen, ist es wichtig, die Grundvorstellungen zu den vier Rechenoperationen zu thematisiert. Beispielsweise sollen die Lernenden die Multiplikation in unterschiedlichen Kontexten erfahren als Wiederholen (zeitlich-sukzessiv), Zusammenfassen (räumlich-simultan) und Vergleichen.

Darstellungen vernetzen
Zudem ist es wichtig, dass Lernende unterschiedliche Darstellungsformen (Material, Bild, Sprache und Mathesprache) kennenlernen und Übertragungen von einer in andere Darstellungsformen regelmäßig nachvollziehen, selbst durchführen sowie sprachlich begründen. Die Übung zum flexiblen Darstellungswechsel unterstützen die Kinder beispielsweise darin, eine Rechenoperationen in der Darstellung eines Bildes oder einer Sachaufgabe zu erkennen oder umgekehrt, einen Term in eine andere Darstellungsform zu übersetzen und z. B. eine eigene Sachaufgabe zu formulieren. Die folgende Grafik verdeutlicht unterschiedliche Darstellungsformen der Multiplikation.
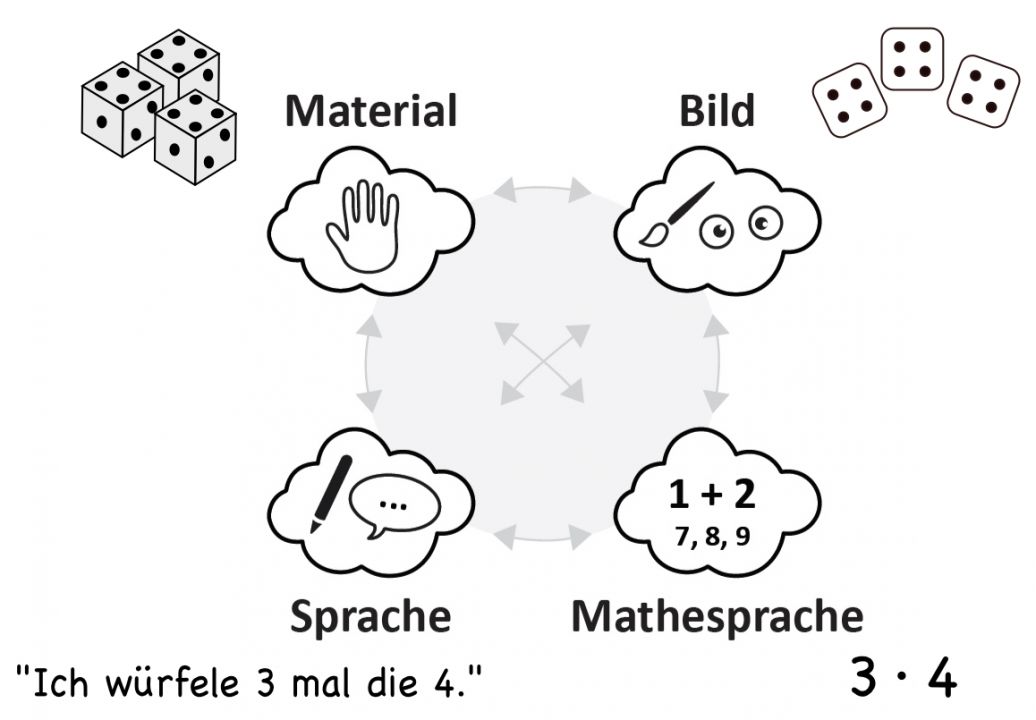
Infotext – Unterrichtsanregungen zur Förderung des Darstellungswechsels
Beziehungen und Strukturen nutzen
Für die Entwicklung eines umfassenden Operationsverständnisses sollen Lernende zudem Gelegenheiten bekommen, Beziehungen und Strukturen entdecken und diese für das sichere und flexible Rechnen nutzen zu können. Materialgestützt bietet die Multiplikation verschiedene Möglichkeiten, Beziehungen und Strukturen zwischen Aufgaben sowie zwischen Rechenoperationen zu erkunden.
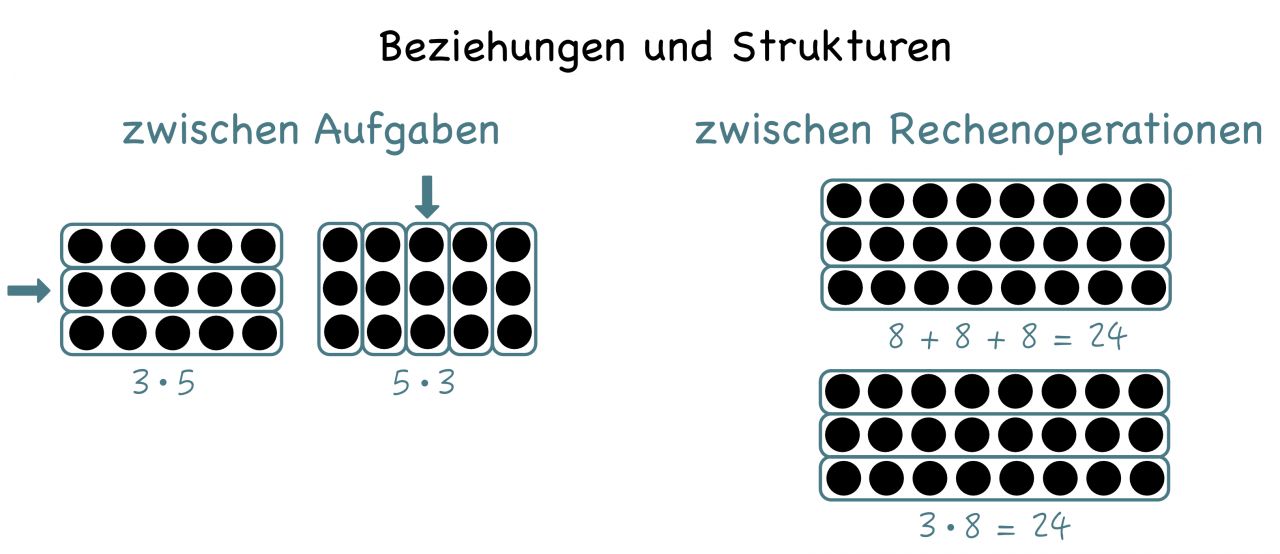
Weiterführende Informationen zum Aufbau eines tragfähigen Operationsverständnisses finden Sie in den nachfolgenden Videos des Projekts DigiMal.nrw:
Hintergrundwissen und Material in den Partnerprojekten
Weiterführenden Informationen zur Vertiefung sowie Material zum Einsatz im Unterricht finden Sie auch auf folgenden Partnerprojektseiten:
primakom
Hintergrundwissen und Unterrichtsmaterialien zum Aufbau eines tragfähigen Operationsverständnisses.
Mathe sicher können (Förderbausteine N3 und N4)
Förderung des Operationsverständnisses mit Hilfe von Diagnose- und Fördermaterial zum Aufbau von Grundvorstellungen zu den vier Grundrechenarten.
KIRA
Hintergrundinformationen und Kinderdokumente zum Aufbau eines tragfähigen Operationsverständnisses.
Mahiko ZR bis 20 und ZR bis 100
Grundlagenwissen zum Aufbau eines tragfähigen Operationsverständnisses in den Modulen "Addition verstehen" und "Subtraktion verstehen"bzw. "Multiplikation verstehen" und "Division verstehen"