Hinweis: Folgende Inhalte und Videos sind im Rahmen des Projekts "MaCo - Mathematik aufholen nach Corona" entstanden.
Warum ist es wichtig, dass Kinder halbschriftlich rechnen können?
Die halbschriftlichen Rechenstrategien stellen zentrale Inhalte des Mathematikunterrichts der Primarstufe dar.
Wichtige Basiskompetenzen, wie beispielsweise die grundlegenden Zahl- und Operationsvorstellungen sowie ein gesichertes Stellenwertverständnis sollten vorab erworben werden, da sie zentrale Verständnisgrundlage für das halbschriftliche Rechnen darstellen.
Darauf aufbauend können in der Schuleingangsphase zunächst die Kompetenzen im Bereich des halbschriftlichen Rechnens erlernt werden, bevor die schriftlichen Rechenverfahren im dritten und vierten Schuljahr thematisiert werden. Zentrales Ziel sollte sein, den flexiblen Umgang mit den unterschiedlichen halbschriftlichen Strategien zu fördern, sodass die Lernenden je nach Aufgabe entscheiden können, welcher Weg am geschicktesten ist bzw. welcher Rechenweg ihnen am sinnvollsten erscheint.
Das Verständnis und der sichere Umgang mit diesen Strategien ist dabei die Basis für die spätere Erarbeitung der schriftlichen Rechenverfahren sowie das Rechnen mit Termen und Formeln in der Sekundarstufe.
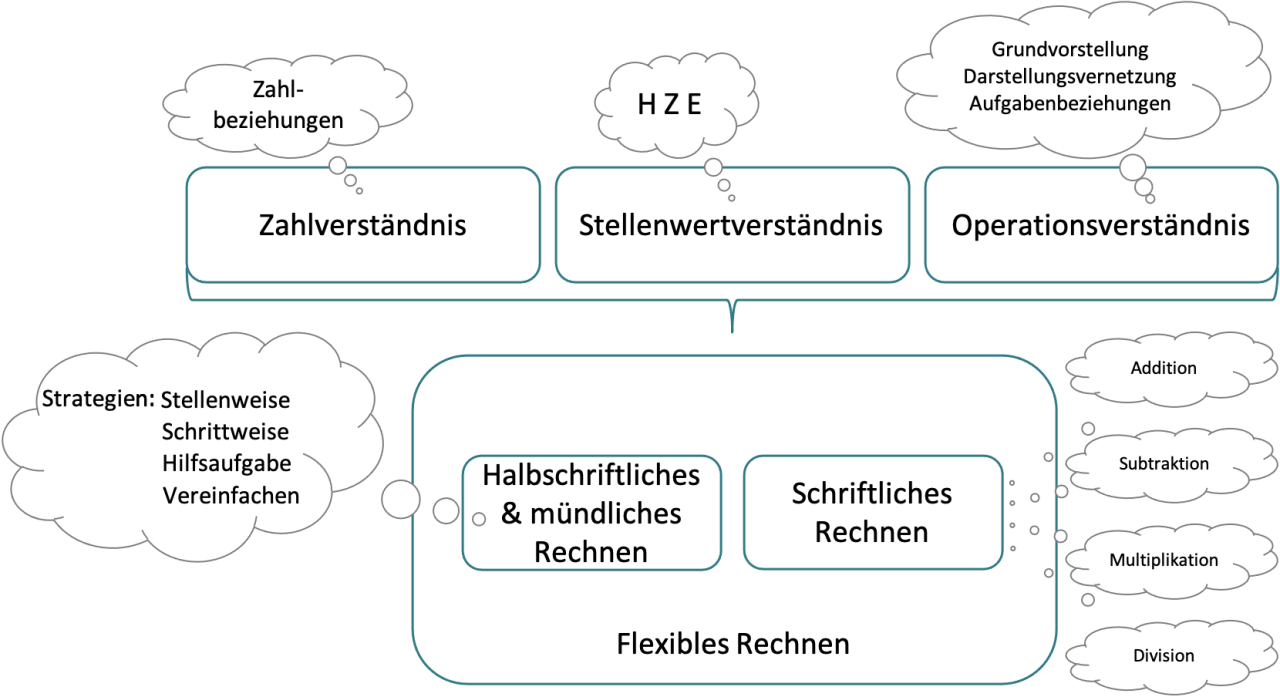
Charakteristisch für das halbschriftliche Rechnen ist, dass der Rechenweg nicht strikt vorgegeben ist, sondern von der Aufgabe und den Präferenzen des jeweiligen Kindes abhängt (Krauthausen & Scherer, 2007, S. 46). Dafür stehen unterschiedliche Lösungsstrategien (Stellenweise, Schrittweise, Hilfsaufgabe, Vereinfachen) zur Verfügung. Die Notation einzelner Zwischenschritte beim Rechnen dient als Merkhilfe, wobei auch hier nicht festgelegt ist, was aufgeschrieben werden muss (vgl. Götze, Selter & Zannetin, 2019, S. 93). Um das inhaltliche Verständnis zu sichern, sollten die unterschiedlichen Strategien stets anschaulich mithilfe von passendem Material erarbeitet werden. Außerdem sollten auch die Vorzüge bzw. Nachteile der jeweiligen Strategie aktiv thematisiert werden, um den sinnvollen Einsatz in Abhängigkeit von Merkmalen einzelner Aufgaben zu fördern.
In den folgenden Videos und Handreichungen werden die verschiedenen Lösungsstrategien in den verschiedenen Grundrechenarten betrachtet und mögliche Schwierigkeiten herausgearbeitet.
Strategie Stellenweise
Um Teilrechnungen mit „glatten“ Zahlen zu erhalten, werden bei dieser Strategie beide Ausgangszahlen stellengerecht zerlegt und anschließend miteinander verrechnet (Götze, Selter & Zannetin, 2019, S. 96). Die dabei entstehenden Teilergebnisse müssen schließlich addiert werden, um das Gesamtergebnis zu berechnen. Diese Strategie ist bei der Division nicht nutzbar.
Strategie Schrittweise
Beim schrittweisen Rechnen wird nur eine der beiden Ausgangszahlen zerlegt, wobei sich die Zerlegung nicht zwingend an den Stellenwerten orientieren muss. Während bei der Addition und Multiplikation frei gewählt werden kann, welcher Wert zerlegt wird, ist bei der Subtraktion und Division festgelegt, dass der Subtrahend bzw. der Dividend zerlegt werden muss.
Strategie Hilfsaufgabe
Hilfsaufgaben werden gebildet, indem die Ausgangsaufgabe geschickt verändert wird, sodass sie einfacher zu lösen ist. Es werden beispielsweise Zahlbeziehungen und Nachbaraufgaben ausgenutzt. Wichtig hierbei ist, dass die genutzte Veränderung am Ende wieder ausgeglichen wird, um das korrekte Ergebnis zu erzielen (vgl. Scherer & Moser Opitz, 2010, S. 153). Hilfsaufgaben bieten sich besonders an, wenn sich glatte Stellenwerte in der Nähe der Ausgangszahlen befinden oder andere benachbarte Zahlen eine einfacherer Rechnung ermöglichen.
Strategie Vereinfachen
Beim Vereinfachen wird die Ausgangsaufgabe so verändert, dass sie sich einfacher lösen lässt. Hier werden beide Ausgangswerte mithilfe der Konstanzgesetze verändert, sodass ein anschließender Korrekturschritt entfällt. Diese Strategie ist in einigen Fällen geschickt, allerdings anspruchsvoller, da sie ein Verständnis der Zahl- und Aufgabenbeziehungen sowie der Konstanzgesetze voraussetzt (vgl. Götze, Selter & Zannetin, 2019, S. 110; Padberg & Benz, 2011, S. 188).
Aufgabenformate zum Üben
Entdeckerpäckchen sind ein häufig eingesetztes Aufgabenformat im Mathematikunterricht. Zunächst wird im ersten Video gezeigt, inwiefern das halbschriftliche Rechnen im Kontext dieses Formats geübt werden kann und Beziehungen dabei erkundet sowie veranschaulicht werden können. In einem zweiten Video werden zudem verschiedene Variationsmöglichkeiten erläutert, die die flexible Anpassung des Formats an individuelle Lernstände ermöglichen.
Video 1: Entdeckerpäckchen
Video 2: Entdeckerpäckchen variieren