Leistungsstarke Lernende
Es gibt nichts Ungerechteres als die gleiche Behandlung von Ungleichen.
Paul F. Brandwein, amerikanischer Psychologe (1912-1994)
Anders als die Intelligenzforschung die intellektuelle Hochbegabung ab einem IQ von 130 definiert, von welcher ca. 2% der Bevölkerung betroffen sind, verstehen wir unter der Förderung von Mathestärken nicht das Privilieg einer Förderung lediglich für hochbegabte Kinder. Die Förderung leistungsstarker Kinder im Fach Mathematik messen wir somit nicht an einem bestimmten IQ-Wert. Jedes Kind hat ein Recht auf Förderung. Besondere Herausforderungen müssen im Unterricht für Kinder geschaffen werden, welche die Basisaufgaben ohne Probleme bearbeiten. Dabei sollte man Kinder im Blick haben, die Aufgaben des Anforderungsbereiches III ohne Schwierigkeiten lösen.
In der Fachliteratur wird die mathematische Begabung als bereichsspezifische Begabung für (produktives) mathematisches Tun verstanden. Wesentliche mathematische Tätigkeiten umfassen dabei – entsprechend dem Verständnis von Mathematik – das Suchen, Bestimmen und Lösen von verschiedenartigen zahlen-theoretischen, algebraischen, geometrischen, stochastischen Einzelproblemen oder komplexen Problemfeldern, das Entwickeln von Strukturen zu diversen Themenfeldern bis hin zum Entwickeln mathematischer Theorien. Für mathematisches Tätigsein sind zugleich ein spielerischer Umgang mit Zahlen und Formen, eine ausgeprägte spezifische mathematische Ästhetik und vielfach sehr enge Wechselbeziehungen zwischen mathematischen und naturwissenschaftlichen Denk- und Arbeitsweisen kennzeichnend. (vgl. Käpnick, 2006, 11f.).
Käpnick formuliert folgende mathematikspezifischen Begabungsmerkmale:
-
Speichern mathematischer Sachverhalte unter Ausnutzung erkannter Strukturen
-
Strukturieren mathematischer Sachverhalte
-
Mathematische Sensibiliät (z.B. Gefühl für Zahlen und geometrische Figuren)
-
Mathematische Fantasie
-
Selbstständiger Transfer erkannter Strukturen
-
Selbstständiges Wechseln der Repräsentationsebenen
-
Selbstständiges Umkehren von Gedankengängen
Im Folgenden werden zu einigen Begabungsmerkmalen exemplarisch Aufgabenbeispiele aufgezeigt:
Strukturieren mathematischer Sachverhalte unter Ausnutzung erkannter Strukturen
Aufgabe
Merke alle Zahlen. Wer kann alle Zahlen korrekt in ein leeres 4x4-Feld eintragen?
Die Kinder haben zum Einprägen der Zahlen 60 Sekunden Zeit. Dann müssen sie die Zahlen in ein leeres 4x4-Feld eintragen.
Das Merken und Wiedergeben aller Zahlen ist nur mit erkannten Zahlstrukturen möglich. So könnte man sich z.B. die vier Eckzahlen 1, 2, 3, 4 merken. Ergänzt wird dann jeweils die darüber oder darunter liegende Zahl zu 10 und die daneben liegende Zahl zu 20. In den vier kleinen 2x2 Quadraten haben die Zahlen in der Diagonalen den Unterschied 10.
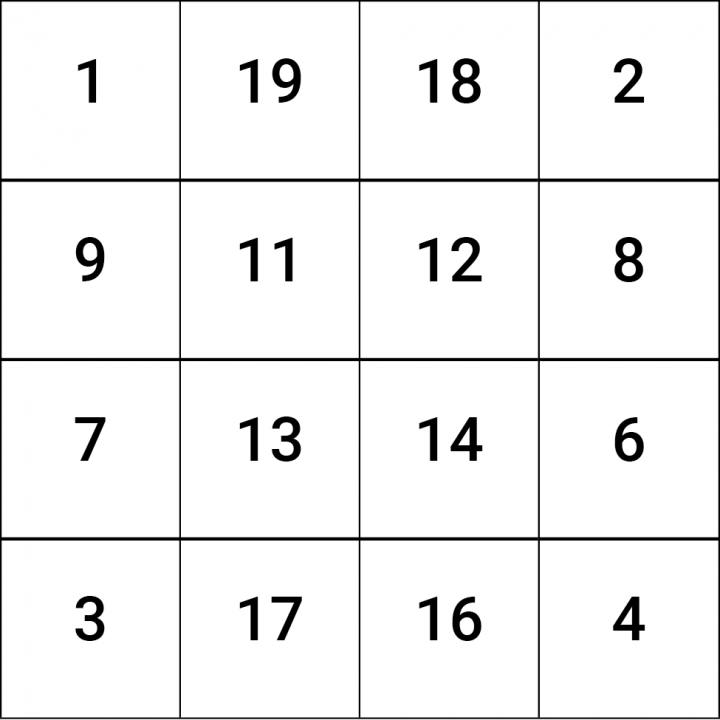
4 x 4 Zahlen merken | vgl. Käpnick, 2006, 12f.
Speichern mathematischer Sachverhalte
Aufgabe
Im nebenstehenden Dreieck kann man Besonderheiten in der Anordnung der Zahlen entdecken.
Welche Besonderheiten erkennst du in der Anordnung der Zahlen? Gib für drei erkannte Besonderheiten Zahlenbeispiele an und beschreibe die Besonderheiten jeweils in einem Satz.
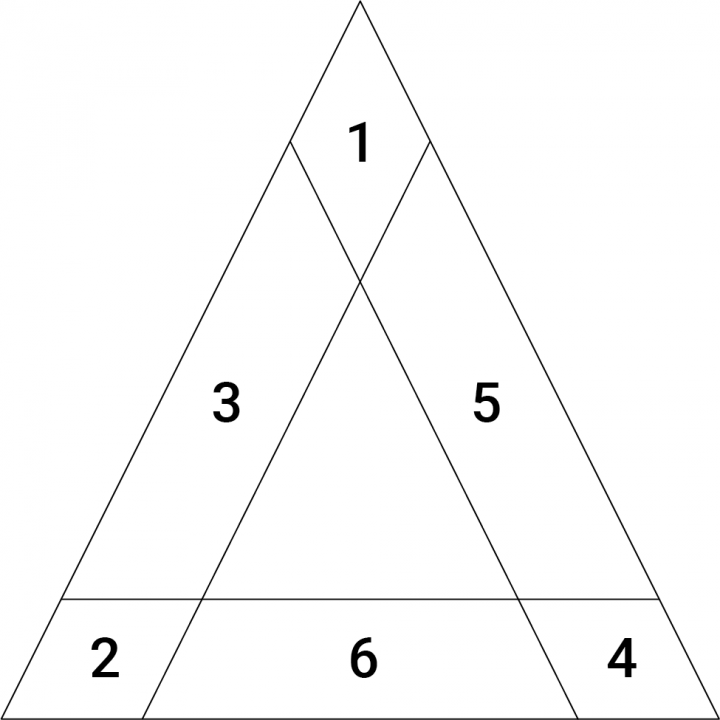
Zahlendreieck | vgl. Käpnick, 2006, 14
Rechenstarke Kinder erkennen im Rahmen dieser Aufgabe vielfältige sinnvolle Zahlenstrukturen, z.B.
-
dass die Summe der drei mittleren Zahlen doppelt so groß ist wie die Summe der drei Eckzahlen
-
dass sich auf der unteren Dreiecksseite drei gerade Zahlen befinden und die drei oberen Zahlen ungerade sind
-
dass man die mittlere Zahl einer Dreiecksseite erhält, wenn man die angrenzenden beiden Eckzahlen addiert
-
dass die mittlere Zahl einer Dreiecksseite plus die gegenüber liegende Eckzahl immer die Summe 7 ergeben
(vgl. Käpnick, 2006, 14f.)
Selbstständiger Transfer erkannter Strukturen - Selbstständiges Wechseln der Repräsentationsebenen - Selbstständiges Umkehren von Gedankengängen
Aufgabe mit Kinderbearbeitung
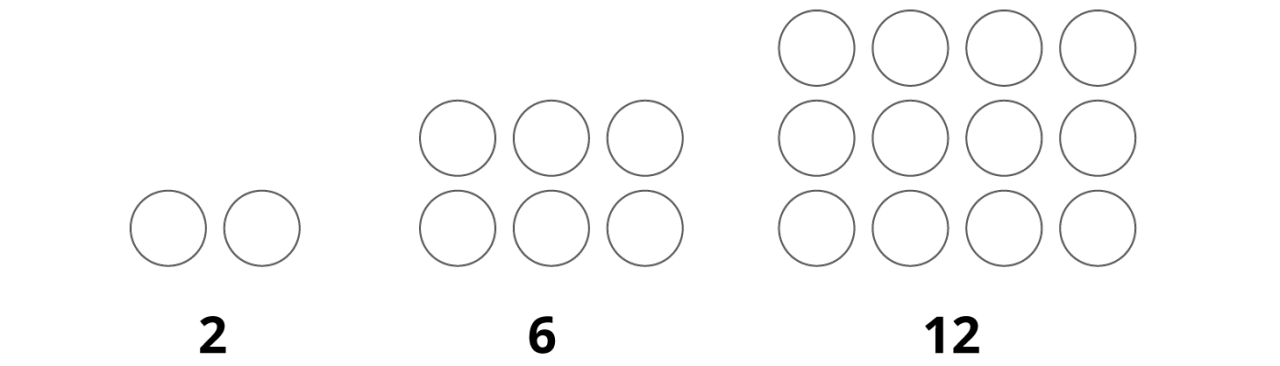
Hier sind die Plättchen so gelegt, dass Rechtecke entstehen.
a) Aus wie vielen Plättchen besteht die nächste Rechteckzahl?
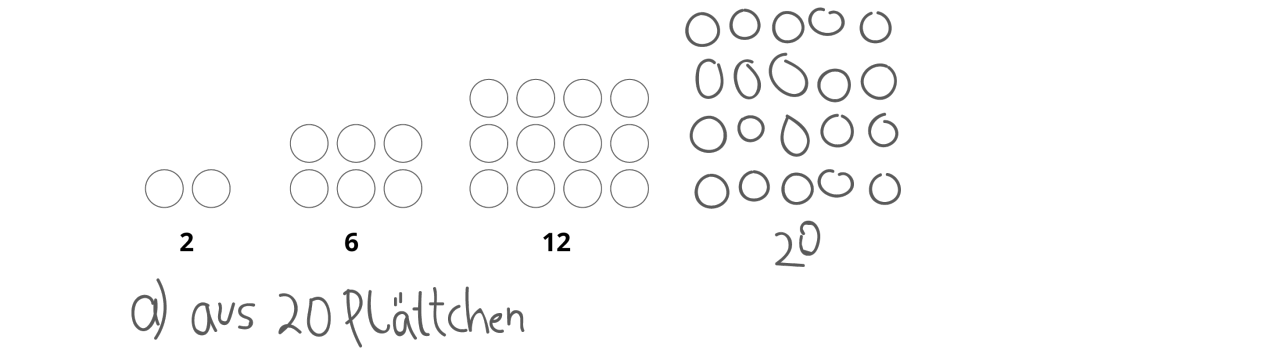
b) Wie verändert sich die Anzahl der Plättchen?

c) Aus wie vielen Plättchen besteht die Rechteckszahl, die 11 Plättchen breit ist?

d) Erfinde ein Zahlenmuster.
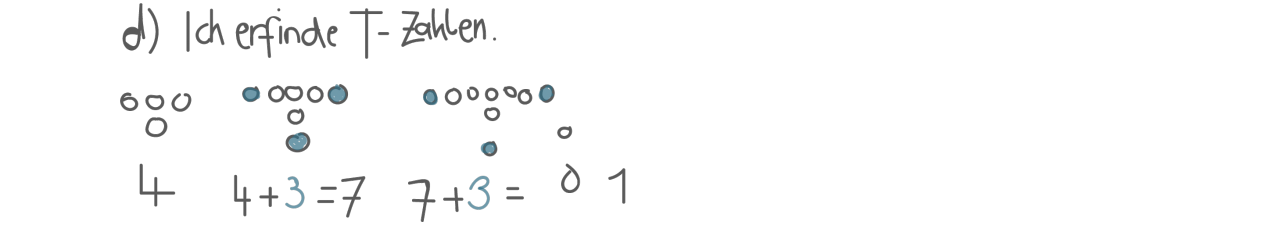
Rechenstarke Kinder finden beim Aufgabenbeispiel "Rechteckzahlen" zu den Aufgabenteilen b) und c) einen sinvollen Lösungsansatz, teilweise mit richtigem Ergebnis. Ein Großteil der Lernenden hat Freude daran, eigene Punktemuster zu erfinden.
Weiteres Material und Informationen zum Thema "Mathestärken fördern" finden Sie hier:
Leistungsstarke im Anfangsunterricht
Im Anfangsunterricht gilt es, leistungsstarke Lernende und ihre besonderen Kompetenzen frühzeitig zu erkennen. Geeignete Diagnoseaufgaben für den Anfangsunterricht ermöglichen die Einschätzung der individuellen Lernstände der Kinder. Mit entsprechenden Lernangeboten kann die Lernmotivation der Kinder weiter gefördert werden. Das Angebot von nur einer Grundaufgabe für alle Lerner kann bei Unterforderung zu Frustrationen führen, welche sich negativ auf die persönliche Einstellung gegenüber dem Mathematikunterricht auswirken könnten.
Durch gute Beobachtung und geeignete Standortbestimmungen lassen sich die Stärken der Kinder erkennen. Für das erste Schuljahr geeignete Standortbestimmungen finden Sie hier: PIKAS: Standortbestimmungen
Aufgabe mit Kinderbearbeitung
1) Male so viele Punkte aus.

2) Zeichne ein Würfelbild.

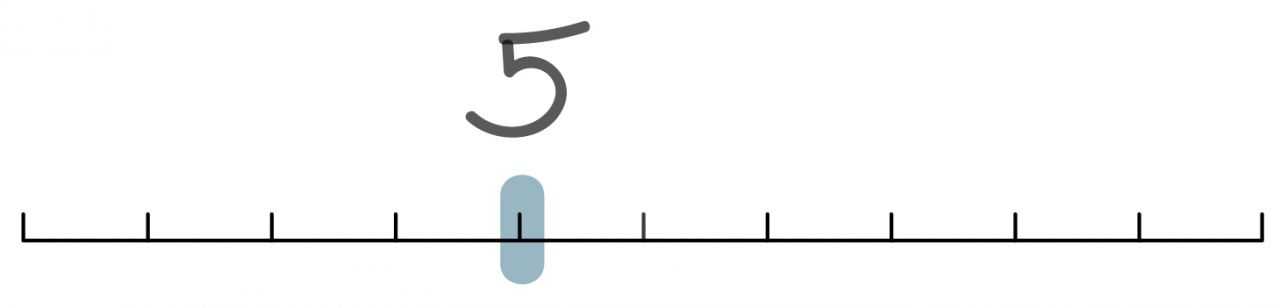
3) Zeige am Zahlenstrahl.
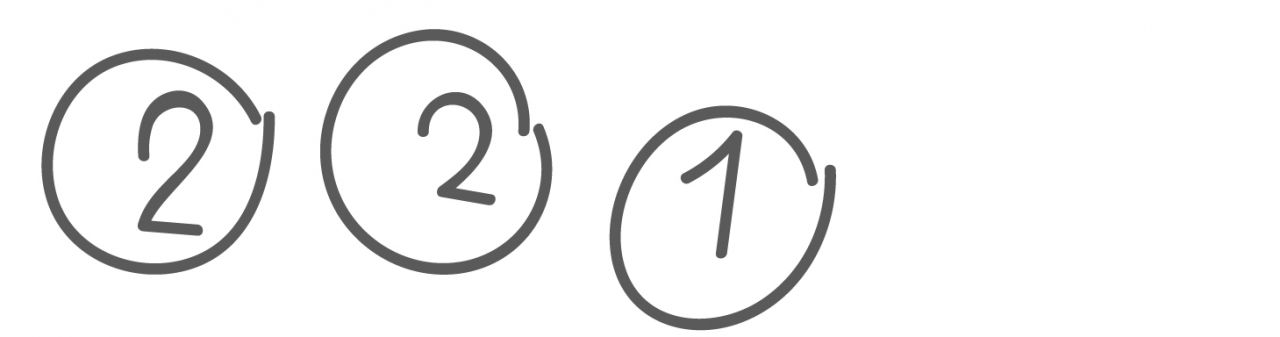
4) Lege mit Geld.
5) Male ein Zahlenbild.

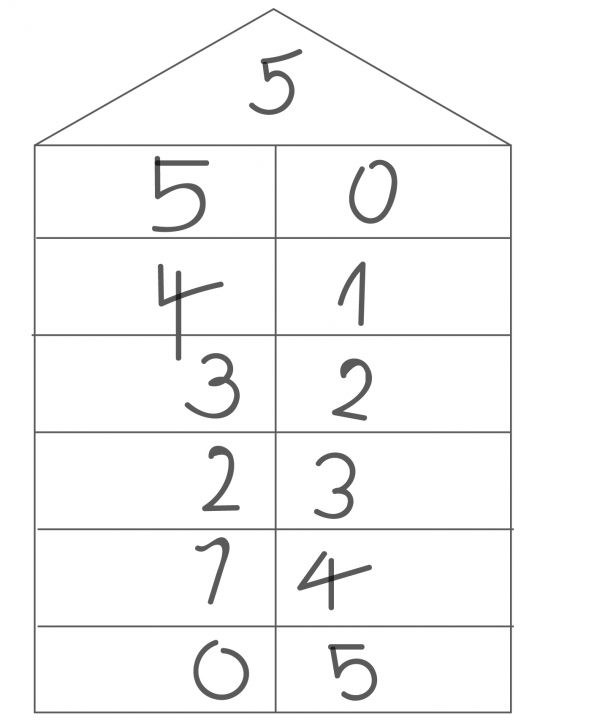
6) Zerlege die Zahl.
7) Schreibe Rechenaufgaben.
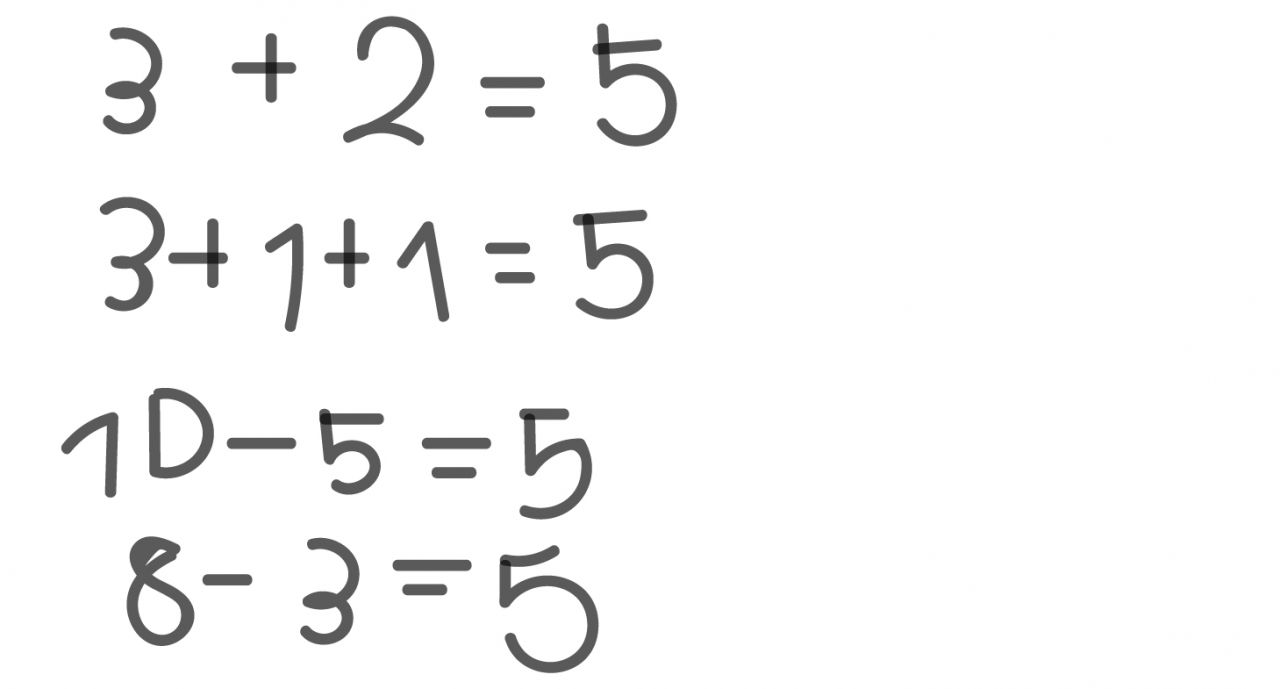
Zahlen unter der Lupe | PIKAS: Arithmetik in der Schuleingangsphase
Die arithmetische Standortbestimmung (SOB) zum Schulanfang (Klasse 1/2) wird direkt zu Beginn eingesetzt. Sie besteht aus einem mündlichen und einem schriftlichen Teil. Besondere Stärken lassen sich so erkennen. Anknüpfend an diese SOB kann eine arithmetische Unterrichtsreihe durchgeführt werden. Diese kann mit Hilfe eines Arbeitsplanes organisiert werden, der anhand der „Übersicht für die Arbeitsplanerstellung" erstellt und individuell an das Kind angepasst werden kann. So ist es möglich, einem leistungsstarken Lerner anstatt einfacher Basisaufgaben, direkt tiefergehende Aufgabenstellungen bearbeiten zu lassen. Die Materialien für die arithmetische Unterrichtsreihe finden Sie im PIKAS: Unterrichtsmaterial Haus 6.
Die Standortbestimmung „Farben, Formen, Folgen" kann auch direkt zu Beginn des ersten Schuljahres eingesetzt werden. Mittels dieser können nicht nur inhaltsbezogene Kompetenzen (Vorkenntnisse zu „Farben und Formen") erhoben werden, sondern auch prozessbezogene Kompetenzen. Hier könnten bei leistungsstarken Kindern die Fähigkeiten im Erkennen von Mustern und Strukturen, ihre bereits vorhandene mathematische Sensibilität und beim Erfinden eigener Muster auch ihre mathematische Kreativität zum Vorschein kommen. Im weiteren Verlauf der Unterrichtsreihe ist es so möglich, die Aufgaben tiefgehender bearbeiten zu lassen. Materialien für eine mögliche Unterrichtsreihe zu diesem Thema („Muster-Werkstatt") finden Sie im PIKAS: Unterrichtsmaterial von Haus 6
Förderung in den Kategorien "eher - tiefer - mehr"
PIKAS unterscheidet die verschiedenen Fördermöglichkeiten in den Kategorien "Mehr, tiefer, eher"
PIKAS: Haus 6 - Fortbildungsmodul 6.2
-
EHER: Mathematisch begabte Kinder bekommen Aufgaben, die die Kompetenzerwartungen höherer Klassenstufen erfüllen. Dies kann mittels Eigenproduktionen auch durch die Kinder selbst geschehen.
-
TIEFER: Alle Kinder einer Lerngruppe bearbeiten nach dem Prinzip der ,natürlichen Differenzierung‘ eine ergiebige Aufgabe.
-
MEHR: Mathematisch begabte Kinder bekommen zusätzliche, sinnvolle Aufgaben, die nicht zwangsläufig in einem direkten Zusammenhang zum aktuellen Lerninhalt der Lerngruppe stehen.
Entsprechend dieser Kategorien werden die Fördermöglichkeiten zu den Aufgabenbeispielen im PIKAS-kompakt-Dorf aufgezeigt und den einzelnen Fachthemen angepasst. Sie finden dazu gezielte Aufgabenstellungen, die Sie leistungsstarken Lernern anbieten können.
Im Folgenden werden die drei Kategorien der Förderung noch näher erläutert.
Förderung im Bereich EHER:
Diese Form der Förderung sollte möglichst nicht durch die Lehrperson initiiert werden. Sie geschieht durch die Kinder häufig in Eigenproduktionen, indem die Kinder die Aufgaben mit selbst gewählten Zahlen in einem höheren Zahlenraum berechnen als dem in ihrer Lerngruppe bereits eingeführten Zahlenraum. Nach dem Spiralprinzip erfolgt eine vergleichbare Thematisierung in der nächsten Klassenstufe. Deswegen ist ein bewusstes Vorgreifen initiiert durch die Lehrperson nur sinnvoll, wenn die Kinder bereits am Mathematikunterricht einer höheren Klasse teilnehmen (Drehtürenmodell).
Förderung im Bereich TIEFER durch natürliche Differenzierung und Aufgabenadaption:
Zu bevorzugen ist immer zuerst die Förderung im Bereich „Tiefer“, da der Lerngegenstand somit für die Lerngruppe identisch ist, nur tiefgehender erfolgt. Geeignet sind für rechenstarke Kinder ergiebige Aufgaben, die es den Kindern ermöglichen, ihre Kompetenzen zu zeigen. Damit eine tiefergehende Bearbeitung möglich ist, erfolgt die Förderung nach dem Konzept der natürlichen Differenzierung. Ist das nicht möglich, besteht die Möglichkeit, die entsprechende Grundaufgabe teilweise zu adaptieren.
Das Konzept der natürlichen Differenzierung wurde von E. Ch. Wittmann entwickelt (vgl. Wittmann, 2010) und verlangt die Differenzierung von „unten“ resp. vom „Kind und vom Fach aus" (vgl. Brügelmann, 2000).
Der Schlüssel dafür liegt in Lernangeboten, die eine niedrige Eingangsschwelle haben, einen bestimmten Grundbestand von Kenntnissen und Fertigkeiten sichern und darüber hinaus den Kindern Optionen ermöglichen, die sie nach ihren individuellen Möglichkeiten wahrnehmen können
Wittmann, 2010, S. 63
Es muss im Gesamtzusammenhang mit den vier anderen Prinzipien ‚Konzentration auf fachliche Grundideen‘, ‚Aktiv-entdeckendes und soziales Lernen‘, ‚Produktives und automatisierendes Üben‘ und ‚systemische Qualitätssicherung‘ gesehen werden, und nur in Verbindung mit diesen Prinzipien kann es seine volle Wirkung entfalten“ (ebd., S. 63).
Alle Kinder arbeiten am gleichen Aufgabenformat, jedes Kind nur auf seinem individuellen Niveau. Im Sinne der natürlichen Differenzierung kommt über die individuellen Lernwege der Kinder ein sozialer Austausch zu Stande, der die individuellen Entwicklungen jedes einzelnen Kindes vorantreiben kann.
Aufgabe
Zeichne alle Formen auf, die du kennst. Schreibe ihre Namen dazu.
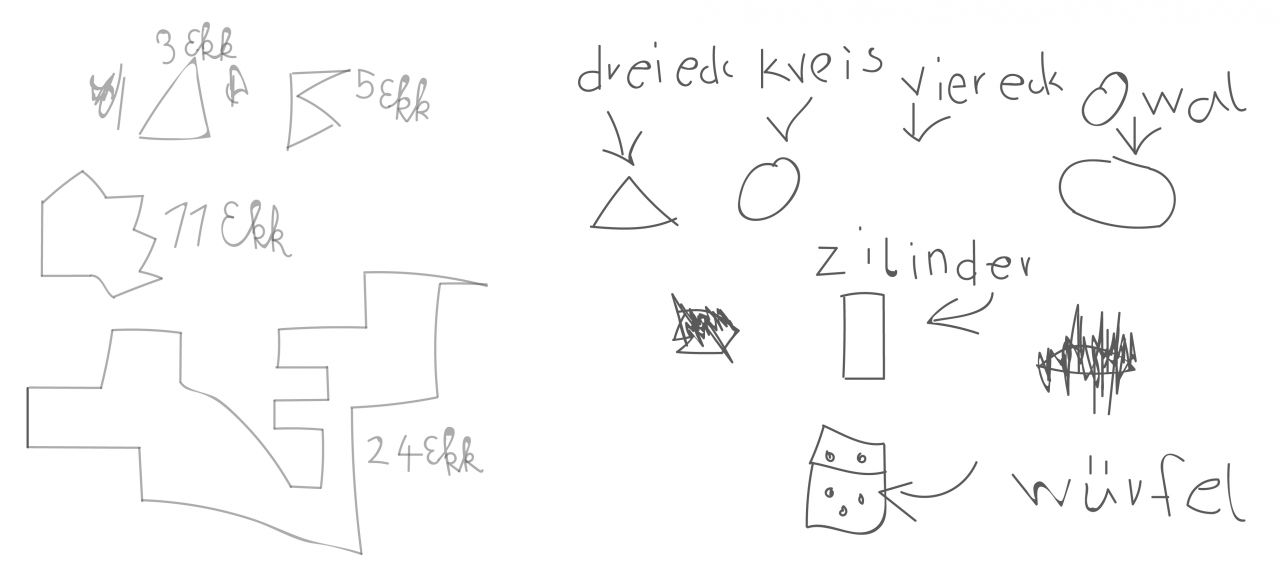
Yara 1. Schuljahr | Gülcan 2. Schuljahr
Nicht immer ist es aber möglich, eine optimale Lernumgebung für alle Kinder über die natürliche Differenzierung zu erreichen.
Deswegen müssen Aufgaben teilweise entsprechend adaptiert werden, um für leistungsstärkere Lerner bearbeitbar zu sein. Alle Kinder lernen somit trotzdem noch an ein und dem selben Lerngegenstand und ein Austausch über ihre Lernwege ist weiterhin möglich.
Eine von der Lehrperson angebotene, offene Grundaufgabenstellung kann jedoch ein Indikator dafür sein, Kinder zu erkennen, welche beispielsweise bereits ein ausgeprägtes Verständnis der Multiplikation besitzen. Daran anknüpfend kann die Lehrkraft weiterführende Aufgaben auswählen.
Aufgabe
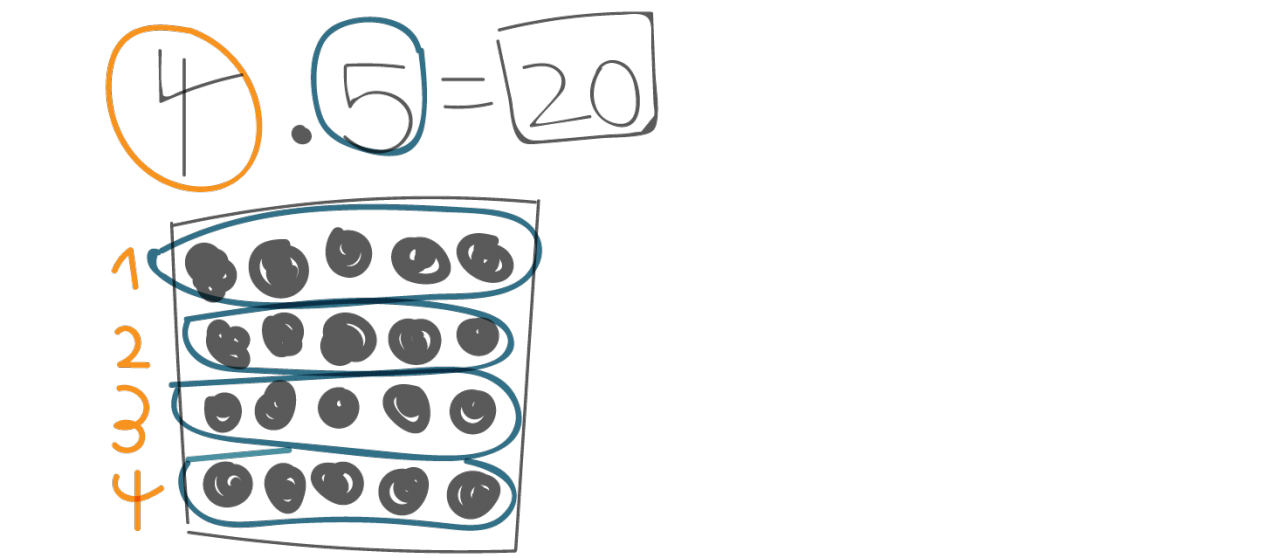
Basisaufgabe Ov. Multiplikation | Yannick, 1. Schuljahr
Hat die Lehrkraft bereits im vorangegangenen Unterricht solche Beobachtung gemacht, sollte diesen Kindern direkt eine weiterführende Aufgabenstellung angeboten werden. Das ständige Angebot von Zusatzaufgaben zusätzlich zu den Grundaufgaben empfinden die rechenstarken Kinder häufig nicht als Belohnung. Geeignet sind ergiebige Aufgaben, die es den Kindern ermöglichen ihre Kompetenzen zu zeigen.
Aufgabe
Ich lege zuerst einen Fünfer und dann nochmal zwei Fünfer darunter. Warum passen die Karten? Erkläre.

Adaption der Basisaufgabe Förderbereich "Tiefer"
Weitere Informationen zur natürlichen Differenzierung finden Sie hier:
Förderung in dem Bereich MEHR durch das Angebot von Knobelaufgaben oder die außerunterrichtliche Förderung:
Ist das gemeinsame Arbeiten an einer Lernaufgabe nach dem Prinzip der "Natürlichen Differenzierung" nicht möglich, sollte der Unterricht angereichert und vertieft werden durch besondere Arbeitsmethoden und Lerninhalte. Dabei sollte ein Zusatzangebot in Form von weiterführenden Themen oder herausfordernden Knobelaufgaben immer den gleichzeitigen Wegfall vertrauter, mechanischer Übungen beinhalten. Denn das Angebot von Aufgaben zusätzlich zur Bearbeitung der Grundaufgaben wird von den Kindern oft nicht als Belohnung empfunden.
Aufgabe
Wie heißt die 10. Rechteckszahl?
Adaption der Basisaufgabe Förderbereich "Mehr"
Weiteres Material für Rechenstarke finden Sie hier:
Leistungsstarke Lernende können auch innerhalb der Schule zu speziellen Gruppen zusammengefasst und in Kursen oder Förderbändern getrennt unterrichtet werden.
Auch die Teilnahme an Mathematikwettbewerben ist für mathestarke Kinder motivierend. Hierzu zählen z.B.
Eine außerunterrichtliche Förderung kann in anerkannten außerschulischen Bildungseinrichtungen den Kindern als Ausgleich verhelfen. Außerschulische Partner verfügen über Expertenwissen und können alternative Angebote machen. Dazu zählen zum Beispiel:
-
Universitäten: Kinder-Uni (Chemie- und Mathematikkurse), Mathe für kleine Asse (WWU Münster)
-
Förderung hochbegabter Kinder in von der BezReg anerkannten außerschulischen Bildungseinrichtungen an Nachmittagen und Bildungstagen
-
Städte und Gemeinden: Kulturelle Angebote, z.B. Musikunterricht, Sportunterricht
-
Elternvereine (Hochbegabung e.V., DGhK, MENSA): Sprachkurse, Forscherkurse
-
Vereine und Clubs: Schachclub, Computerclub, …
-
Mathematische Sommerakademie
Leitfaden für Lehrkräfteteams
befindet sich derzeit in Arbeit
Fazit
Förderung begabter Kinder sollte in der Regel gemeinsam mit anderen Kindern der Lerngruppe erfolgen, denn auch sie brauchen:
-
kooperativ-kommunikative Lernumgebungen
-
den fachlichen Austausch mit anderen Kindern
-
die ganze Lerngruppe als Forum für die Darstellung ihrer Ideen und Denkweisen
→ Aber: auch äußere Differenzierung z. B. in einer ,Mathe Knobel AG‘ oder bei Mathematikwettbewerben ist sinnvoll