Im Lehrplan wird gefordert, dass komplexe fachbezogene Kompetenzen in den Klassenarbeiten der Klassen 3 und 4 überprüft werden. Dies bedeutet, dass inhalts- und prozessbezogene Kompetenzen gleichermaßen ihren Platz in den Klassenarbeiten finden müssen.
Zudem verlangen die Richtlinien, dass Kinder im Sinne eines pädagogischen Leistungsverständnisses ausgehend von ihren individuellen Voraussetzungen sowie durch Ermutigung und Unterstützung ihre Leistungsfähigkeit erproben und weiterentwickeln und so Vertrauen in ihre eigene Leistungsfähigkeit gewinnen können.
Das Materialpaket gibt Beispiele dafür, wie Klassenarbeiten im Sinne der Forderungen der Richtlinien und des Lehrplans verändert werden können. Sie erhalten Anregungen zur Erstellung differenzierter Klassenarbeiten („Klassenarbeiten: differenziert!") sowie Informationen zum Thema „Probearbeiten". Zudem werden im Text zu „Profi-Mathearbeiten" acht Bausteine vorgestellt, die Sie und Ihr Kollegium darin unterstützen können, prozessbezogene, offene und informative Mathematikarbeiten zu entwickeln.
Bei differenzierten Arbeiten geht es nicht darum, von allen Schülerinnen und Schülern innerhalb eines vorgegebenen Zeitraums dieselben Leistungen zu erwarten. Vielmehr erhalten die Kinder ein differenziertes Aufgabenangebot, das sich sowohl auf grundlegende als auch auf weiterführende Anforderungen bezieht.
So kann jedes Kind diejenigen Aufgaben auswählen, die seinem Leistungsstand eher entsprechen. Für schwächere Schülerinnen und Schüler soll das Konzept der differenzierten Arbeiten dabei unterstützen, zunächst im Bereich der Grundanforderungen Sicherheit zu erwerben und nicht durch den Vergleich mit leistungsstärkeren Kindern zu „Versagern" zu werden.
Daher können differenzierte Arbeiten einen Beitrag dazu leisten, Versagensängste abzubauen und Frustrationsgefühle in Bezug auf das Fach Mathematik vorzubeugen. Den Kindern wird es im Vergleich zu herkömmlichen Arbeiten leichter ermöglicht, ein positives Selbstbewusstsein in Bezug auf die eigene Leistung auf- bzw. auszubauen.
Die Differenzierung kann dabei u.a. nach folgenden Kriterien erfolgen (vgl. Sundermann & Selter 2011, S. 164):
-
Anzahl der (Teil-)Aufgaben,
-
Schwierigkeitsgrad der Aufgabendaten (Zahlenraum, Rechenanforderungen, ...),
-
Komplexität der Aufgabenstellung (Anzahl der Lösungsschritte, Abstraktionsgrad, ...),
-
Präsentationsform (Textmenge, unterstützende Abbildungen, Existenz von Hilfsaufgaben oder Beispielen ...),
-
Grad der erforderlichen Transferleistungen,
-
Grad der Anforderungen beim Beschreiben und Begründen, sowie
-
Zeitpunkt (nicht alle Kinder müssen zum gleichen Zeitpunkt die gleichen Leistungen erbringen).
Im Folgenden werden drei verschiedene Modelle differenzierter Klassenarbeiten vorgestellt, wobei das erste Modell in zwei Varianten beschrieben wird: Die zweite Variante stellt eine Modifikation der ersten dar, ohne deren Nachteile zu haben. Das Sternchenaufgaben-Modell, auch als Fundamentum-Additum-Modell bekannt (vgl. auch Wuschansky 1989), lehnt sich an die Vorschläge zu differenzierten Diktaten an. Im ersten, größeren Teil der Arbeit (ca. zwei Drittel des Gesamtumfangs) sind diejenigen Aufgaben zu finden, die den grundlegenden Anforderungen zuzuordnen sind. Der zweite, kleinere Teil (ca. ein Drittel des Gesamtumfangs) besteht aus Aufgaben mit weiterführenden Anforderungen.
Die weiterführenden Anforderungen sind durch ein Sonderzeichen (Sternchen, Blitz, Gewicht, …) gekennzeichnet. Die Kinder können sich nun zunächst auf die Grundanforderungen konzentrieren und anschließend einzelne oder alle Aufgaben der weiterführenden Anforderungen bearbeiten.
Bei der nachstehenden (inhaltlich nicht sonderlich substanziellen) Beispiel-Arbeit konnten die Kinder bei Erfüllung der Grundanforderungen 30 von 44 insgesamt möglichen Punkten erreichen. Werden diese 30 Punkte bzw. ca. 2/3 der Gesamtpunktzahl erreicht, entspricht das als Zensur der Note „befriedigend".
Als problematisch an diesem Modell hat sich herausgestellt, dass zumindest einige der schwächeren oder der langsamer arbeitenden Kinder nach zwei Dritteln der Arbeit aufhören, da sie denken, dass die folgenden Aufgaben für sie ohnehin zu schwierig sind oder sie keine Zeit mehr haben.
Bei manchen Kindern reicht auch die Konzentrationsfähigkeit nicht mehr aus, um sich nach der Bearbeitung des grundlegenden Teils noch produktiv mit den anspruchsvolleren Aufgaben auseinanderzusetzen.
Probearbeiten (vgl. Sundermann & Selter 2011, S. 157ff.) können eine Möglichkeit sein, den Umgang mit Klassenarbeiten zu verändern. So können sie den Stellenwert solcher Klassenarbeiten als herausgehobene und bisweilen mit negativen Assoziationen und Stress behaftete Form der Leistungsmessung relativieren, indem sie den Kindern vorab aufzeigen, was auf sie zukommt.
Eine Probearbeit wird im zeitlichen Abstand von 7 bis 10 Tagen vor der eigentlichen Klassenarbeit geschrieben und ist nichts anderes als ein Test unter „Ernstfallbedingungen".
Die Lehrkraft sieht die Probearbeiten der einzelnen Kinder durch, korrigiert sie und gibt sie zurück. Die beurteilungsrelevante Hauptarbeit wird dann einige Tage später geschrieben – je nach aufgetretenen Schwierigkeiten. Die Hauptarbeit wird in der Regel analog aufgebaut...
-
gleiches Layout
-
gleiche Aufgabenformate
-
vergleichbare Zahlenwerte bzw. Rechenanforderungen (z. B. Rechnen mit der 0)
-
gleiche Stufung der Anforderungen bzw. Schwierigkeiten
-
gleiche Bepunktung
Wozu überhaupt Mathematikarbeiten?

Mathematikarbeiten können grundsätzlich zwei Funktionen erfüllen.
Zum einen können sie im Dienste der Überprüfung und der nachfolgenden Selektion geschrieben werden. Nicht wenige der herkömmlichen Arbeiten fragen meist nur leicht abprüfbare Kenntnisse und Fertigkeiten aus dem Bereich Zahlen und Operationen ab.
Sie sind nicht selten ergebnisorientiert und nicht prozessbezogen. Wenn der Lösungsweg in die Bewertung einbezogen wird, geht es häufig darum, dass die Kinder einen ganz bestimmten Weg wählen, der eingeübt wurde. Es steht den Kindern nicht offen, wie sie die Aufgabe bearbeiten. Veranschaulichen lässt sich dies nach Sundermann und Selter (2011) an dem unten stehenden Würfel, der aus acht kleineren Würfeln besteht. Mathematikarbeiten im oben genannten Sinne würden dabei dem links, oben und vorne liegenden Würfel (nicht prozessbezogen, nicht offen, nicht informativ) zugeordnet werden.
Andererseits können Mathematikarbeiten dazu dienen, dass Lehrpersonen mehr vom Denken der Schülerinnen und Schüler erfahren, auch um sie nachfolgend im weiteren Lernprozess unterstützen zu können. Durch die Auswertung der Mathematikarbeit sollte dabei die Lehrkraft erkennen können, in welchen Bereichen einzelne Kinder gefördert und gefordert werden sollten. Außerdem wird ihr so eine Rückschau auf den bisherigen Unterricht ermöglicht und die Planung des zukünftigen Unterrichts bzw. das Ergreifen spezieller Förder- und Fordermaßnahmen für einzelne Kinder erleichtert.
Wenn Mathematikarbeiten in diesem Sinne fungieren sollen, ist es notwendig, dass sie, so wie der Lehrplan es fordert, komplexe fachbezogene Kompetenzen überprüfen, damit sie aufschlussreiche Informationen über die gesamten mathematischen Kompetenzen der Kinder liefern können.
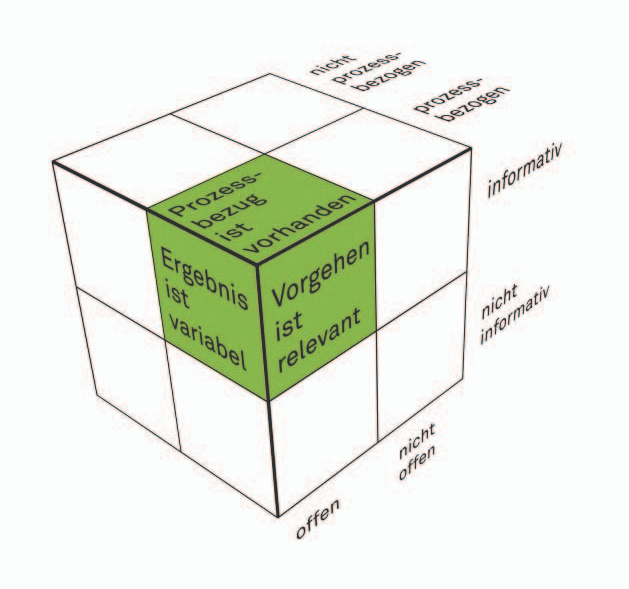
Daher ist es notwendig, dass der Lösungsprozess sichtbar wird. Das Ergebnis alleine verrät zu wenig über die Vorgehens- und Denkweisen der Kinder. Es ist nicht so wichtig, wie viele Fehler das Kind macht, sondern welche Fehler es macht und welche Kompetenzen und Defizite das Kind hat. Zudem müssen die Aufgaben offene Herangehensweisen der Kinder zulassen, da die individuelle Nutzung und Auswahl von Lösungsprozessen Einblick in die Kompetenzen der Kinder zulässt. Hierzu sind offene, informative und prozessbezogene Aufgaben notwendig.
Das gesamte Material (2,4 MB) dieser Seite können Sie gebündelt herunterladen