Forscherhefte
Forscherhefte im Mathematikunterricht ermöglichen ein selbstgesteuertes forschend-entdeckendes Lernen. Sie sind kein eindeutig definiertes Arbeitsmittel. In der offensten Form sind es leere Hefte, in die die Kinder ihre mathematischen Erfindungen und Entdeckungen zu selbstgewählten Inhalten als „freie mathematische Texte“ eintragen.
Das Forscherheft ist einerseits ein Instrument, um sich möglichst selbstständig mathematische Sachverhalte zu erschließen: Die Kinder äußern Vermutungen, variieren Zahlen systematisch, analysieren Veränderungen, vergleichen, untersuchen Zusammenhänge, dokumentieren Beobachtungen, suchen nach Erklärungen etc.
Für die Kinder ist das Forscherheft aber zugleich auch ein persönliches Dokument ihrer (fortschreitenden) Entdeckungen und Erkenntnisse. Im Gegensatz zu einer losen Sammlung von Arbeitsblättern gibt das Forscherheft den Kindern einen Überblick über die Gesamtheit aller Aufgabenstellungen. Vor allem aber bewirkt es, dass sich die Kinder mit „ihrem“ Heft in zunehmendem Maße identifizieren und stolz sind auf ihre Einträge.
Forscherhefte ermöglichen den Schülerinnen und Schülern, sich eigenständig mit herausfordernden, problemhaltigen Aufgaben im Sinne eines aktiv-entdeckenden Lernens auseinanderzusetzen. Durch Forscheraufträge, die in Kleingruppen (den sogenannten „Forscherrunden“) durchgeführt werden, findet ein sozialer Austausch unter den Kindern statt. Die Kompetenz des „Argumentierens" und „Kommunizierens“ wird auf diese Weise gefördert.
Die vorliegenden Materialpakete zeigen Ihnen an konkret ausgearbeiteten Beispielen zum Aufgabenformat „Mal-Plus-Haus“ sowie „Mal-Mühle“, wie ein Forscherheft im Unterricht transparent und sinnstiften eingesetzt werden kann.
Mal-Plus-Haus
Inhalt
Überblick
Basisinfos
Forscherheft „Mal-Plus-Haus"
Einheit 1: „Wie passen die Zahlen in dieses Haus?"
Einheit 2: „Ein Mal-Plus-Haus zum Knobeln"
Einheit 3: Wir forschen gemeinsam: „Ein Mal-Plus-Haus zum Knobeln"
Forscherrunden
Einheit 4: Kennen wir eine Strategie? „Ein letztes Mal-Plus-Haus zum Knobeln"
Überblick
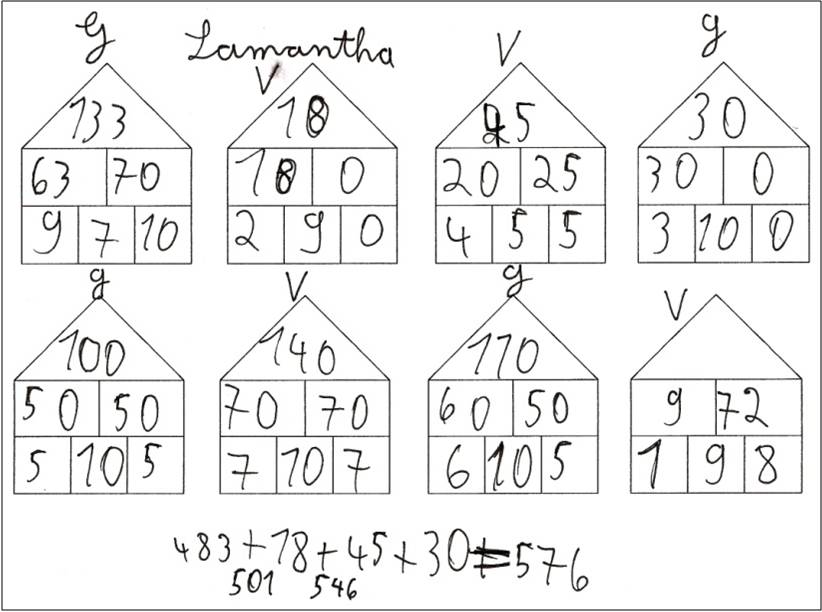
Forscherhefte im Mathematikunterricht ermöglichen ein selbstgesteuertes forschend-entdeckendes Lernen im Mathematikunterricht. Das vorliegende Materialpaket zeigt am Beispiel einer Unterrichtsreihe zum Aufgabenformat „Mal-Plus-Haus", wie ein Forscherheft im Rahmen einer Unterrichtsreihe transparent und sinnstiftend eingesetzt werden kann. Das „Mal-Plus-Haus" ist ein Aufgabenformat, mit dem – neben der Addition und Subtraktion – das kleine Einmaleins operativ durchgearbeitet und intensiv geübt werden kann. Durch die Auseinandersetzung mit den unterschiedlichsten Forscheraufträgen erarbeiten sich die Schülerinnen und Schüler eigenständig die Struktur des „Mal-Plus-Hauses" und entdecken das Distributivgesetz noch einmal in einem völlig neuen Kontext. Die Unterrichtsreihe liefert mit ihrem umfangreichen Lehrer- und Schüler-Material zahlreiche weitere methodische Anregungen für einen lernfördernden Mathematikunterricht.
Basisinfos
Die Basisinfo zum Forscherheft „Mal-Plus-Haus" beschreibt allgemein die Funktion eines Forscherheftes und charakterisiert die Forscheraufträge im Forscherheft „Mal-Plus-Haus". Es wird aufgezeigt, wie ein Forscherheft für die Schülerinnen und Schüler sinnstiftend eingeführt werden kann und welche methodische Rahmung bei der Einbindung des Forscherheftes in eine Unterrichtsreihe bedacht werden muss.
Die Sachinfo zum „Mal-Plus-Haus" schlüsselt die mathematische Struktur des Aufgabenformats auf und erläutert die fachlichen Hintergründe der einzelnen Forscheraufträge.
Detaillierte Informationen zu einer Unterrichtsreihe mit einem Forscherheft zum „Mal-Plus-Haus" finden Sie hier.
|
|
Basisinfos – Forscherheft |
|
|
Sachinfos – Mal-Plus-Haus |
Forscherheft „Mal-Plus-Haus"
|
|
Schülermaterial – Forscherheft |
|
|
Schülermaterial – Leerformate Mal-Plus-Haus |
Einheit 1: „Wie passen die Zahlen in dieses Haus?"
In der ersten Einheit erarbeiten sich die Schülerinnen und Schüler den Aufbau des „Mal-Plus-Hauses" selbstständig und handlungsorientiert. Einfache Rechenübungen mit dem Aufgabenformat geben den Kindern Sicherheit darin, die Zahlen im „Mal-Plus-Haus" richtig miteinander zu verknüpfen.
Lehrer-Material
Schüler-Material
|
|
Material 1 bis 4 – Wie wird im Haus gerechnet? |
|
|
Arbeitsblatt 1 und 2 – Mal-Plus-Häuser berechnen |
Einheit 2: „Ein Mal-Plus-Haus zum Knobeln"
Die Schülerinnen und Schüler sollen Transparenz für die Auseinandersetzung mit den Forscheraufträgen des Forscherheftes erhalten. Die Kinder versuchen ein „Knobel-Haus" zu lösen. Sie stellen fest, dass sie zumeist mehrere Versuche benötigen. Daraus wird die Fragestellung abgeleitet, ob es eine sichere Strategie für die Lösung einer solchen Problemstellung gibt. Diese Frage gibt die Zielrichtung für das Forschen im Forscherheft vor.
Lehrer-Material
Schüler-Material
|
|
Arbeitsblatt 1 und 2 – Ein Mal-Plus-Haus zum Knobeln |
|
|
Selbsteinschätzungsbogen – Ein Mal-Plus-Haus zum Knobeln |
|
|
Sprachhilfen für den Selbsteinschätzungsbogen – Ausdrücke |
Einheit 3: Wir forschen gemeinsam: „Ein Mal-Plus-Haus zum Knobeln"
In einer gemeinsamen Forscherstunde lösen die Kinder ein weiteres „Knobel-Haus". Sie wenden Techniken wie vergleichen, sortieren und überprüfen an. Gemeinsam wird mit den Kindern die Beziehung zwischen den „Kellerzahlen" und der „Dachzahl" herausgearbeitet und veranschaulicht.
Lehrer-Material
Schüler-Material
|
|
Arbeitsblatt 1 und 2 – Ein Mal-Plus-Haus zum Knobeln |
|
|
Ausschneidebogen – Mal-Plus-Häuser zum Sortieren |
Forscherrunden
Forscherrunden sind wichtig, um den Austausch über die individuellen Forschungsergebnisse anzuregen. Durch einen gemeinsamen „Forscherrunden-Auftrag" vertiefen die Kinder ihre Erkenntnisse.
Lehrer-Material
Schüler-Material
|
|
Leitfaden – Forscherrunde |
|
|
Forscherbericht – Forscherrunde |
|
|
Forscherauftrag 4 – Forscherrunde |
|
|
Forscherauftrag 5 – Forscherrunde |
|
|
Forscherauftrag 9 – Forscherrunde |
Einheit 4: Kennen wir eine Strategie? „Ein letztes Mal-Plus-Haus zum Knobeln"
Die Kinder erhalten ein ähnliches „Knobel-Haus" wie in Einheit 2. Sie werden dieses Haus nun schneller lösen und zumeist gezielt eine Strategie anwenden, um möglichst viele Möglichkeiten zu finden. Die eigenen Lernfortschritte werden den Kindern bewusst. Eine Abschlussreflexion und das Würfelspiel „Die höchste Dachzahl gewinnt" beenden die Unterrichtsreihe.
Lehrer-Material
Schüler-Material
|
|
Reflexionsbogen – Mal-Plus-Häuser zum Knobeln |
|
|
Leerformate – Wer erreicht die größte Dachzahl? |
|
|
Arbeitsblatt – Ausprobieren und richtige Lösung einkreisen |
 |
Hier finden Sie das gesamte Material dieser Seite (5,5 MB). |
Mal-Mühle
Inhalt
Überblick
Sachinfos
Forscherheft „Mal-Mühle“
Forscherrunden
Überblick
Forscherhefte ermöglichen den Schülern, sich eigenständig mit herausfordernden, problemhaltigen Aufgaben im Sinne eines aktiv-entdeckenden Lernens auseinanderzusetzen. Durch Forscheraufträge, die in Kleingruppen (den sogenannten „Forscherrunden“) durchgeführt werden, findet ein sozialer Austausch unter den Schülern statt. Die Kompetenz des „Argumentierens" und „Kommunizierens“ wird auf diese Weise gefördert.
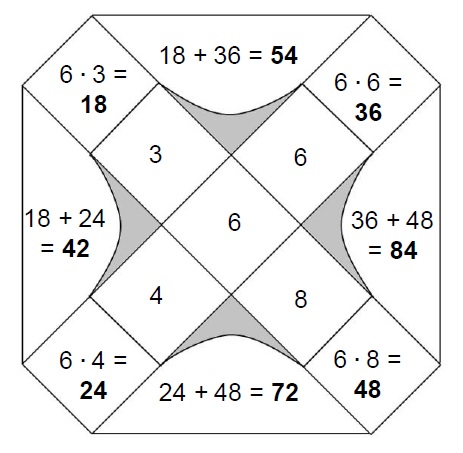
Die Mal-Mühle ist ein Aufgabenformat, mit dem sich in erster Linie das kleine Einmaleins intensiv üben und festigen lässt. Indem die Schülerinnen und Schüler das Distributivgesetz zur Berechnung bestimmter Zahlen nutzen, wird in gewissem Umfang auch das große Einmaleins behandelt.
Die „Mal-Mühle“ stellt eine Erweiterung des Aufgabenformates „Mal-Plus-Haus“ dar. Es bietet sich daher an, das Forscherheft „Mal-Mühle“ zur vertiefenden Übung des Einmaleins in Jahrgang 3 oder 4 einzusetzen.
Sachinfos
In den Sachinfos zur „Mal-Mühle“ werden die fachlichen Hintergründe des Aufgabenformates aufgezeigt. Der Aufbau wird erläutert. Ebenso finden sich dort mögliche Aufgabenstellungen zur „Mal-Mühle“ wieder, von denen eine Auswahl im Forscherheft enthalten ist.
|
|
Sachinfos – Mal-Mühle |
Forscherheft „Mal-Mühle“
Zu Beginn der Arbeit mit dem Forscherheft bietet es sich an, die Schüler Vermutungen zum Aufbau der Mal-Mühle äußern zu lassen: Nach welchen Regeln wird die Mal-Mühle ausgefüllt? Hierzu können die beiden Mal-Mühlen auf dem Deckblatt des Forscherheftes genutzt werden. Während eine Mal-Mühle bereits ausgefüllt ist, kann die zweite gemeinsam im Klassenverband ergänzt werden. Anschließend können sich die Schüler eigenständig mit den Aufgaben im Forscherheft befassen und nach und nach die Besonderheiten der Mal-Mühle entdecken.
Lehrer-Material
|
|
Lösungsheft – Forscherheft zur Mal-Mühle |
Schüler-Material
|
|
Forscherheft – Mal-Mühle |
|
|
Leerformate – Mal-Mühle |
Forscherrunden
Damit sich die Schüler über ihre individuellen Entdeckungen austauschen, werden die Forscheraufträge 3, 5 und 8 in Kleingruppen, den sogenannten Forscherrunden, bearbeitet.
Lehrer-Material
|
|
Plakat – Ablauf |
|
|
Plakat 10 – Forscherrunde (farbig) |
|
|
Plakat 10 – Forscherrunde (schwarz-weiß) |
Schüler-Material
|
|
Leitfaden – Forscherrunde |
|
|
Forscherbericht – Forscherrunde |
 |
Hier finden Sie das gesamte Material dieser Seite (2,7 MB). |