gelöscht-Vorstellungen aufbauen
Überblick
Die folgenden Seiten widmen sich der Frage, wie Vorstellungen im Arithmetikunterricht aufgebaut werden können, damit Kinder bei der Überwindung von Rechenschwierigkeiten unterstützt werden können.
Hierzu wird
- das Vierphasenmodell anhand des Aufbaus von Zahlvorstellungen beschrieben,
- die Ablösung vom zählenden Rechnen aufgegriffen,
- auf die Entwicklung des Stellenwertverständnisses eingegangen,
- der Aufbau von Operationsvorstellungen thematisiert und
- aufzeigt, wie „Guter Umgang mit Darstellungsmitteln" erzielt werden kann.
Vierphasenmodell
Probleme beim Mathematiklernen sind häufig durch das Fehlen grundlegender Vorstellungen zu Zahlen, Rechenoperationen und -strategien begründet. Zwar sind Lernende mit Rechenschwierigkeiten, denen es an solchen Vorstellungen fehlt, häufig in der Lage, bestimmte Verfahren anwenden zu können, allerdings verhindern fehlende Vorstellungen, dass sie auch verstehen, warum sie gerade so vorgehen können und dürfen, wie sie es tun.
Um Kinder dabei zu unterstützen, Vorstellungen aufbauen zu können, hat sich das Vierphasenmodell (vgl. Schipper, Wartha & von Schroeders 2011; Wartha & Schulz 2013) bewährt. Der Grundgedanke dieses Modells besteht darin, konkrete Materialhandlungen gedanklich vollziehen zu können. Anfängliche Handlungen am Material werden nach und nach zugunsten mentaler Vorstellungen abgelöst. Die nachstehende Abbildung beschreibt die Aktivitäten der einzelnen Phasen des Modells allgemein.

Das Vierphasenmodell (Abbildung aus Wartha & Schulz, 2011, S. 11)
Im weiteren Verlauf dieser Seite wird gezeigt, wie der Aufbau von Vorstellungen anhand des Vierphasenmodells gelingen kann. Hierzu wird exemplarisch die nicht-zählende Zahldarstellung am Zwanzigerfeld fokussiert. Es wird aufgezeigt, wie Kinder auf dem Weg von der konkreten Zahldarstellung mit Plättchen am Zwanzigerfeld zum gedanklichen Handeln im Unterricht unterstützt werden können.
Phase 1: Das Kind handelt am geeigneten Material.
In Phase 1 operiert das Kind mit Material, das für die aufzubauende Vorstellung geeignet erscheint. Für die nicht-zählende Zahldarstellung können hierzu das Zwanzigerfeld sowie Plättchen herangezogen werden. Alternativ wäre es jedoch auch denkbar, den Rechenrahmen heranzuziehen. Je nach dem, welches Arbeitsmittel genutzt wird, sind passende nicht-zählende Handlungen vom Kind vorzunehmen. So wäre es für die Darstellung der Zahl 17 zentral, Plättchen nicht nur einzeln nacheinander zu legen. Vielmehr ist es wichtig, auch Zehner- und Fünferstreifen zu verwenden, um die Beziehungen der darzustellenden Zahl zur Fünf und zur Zehn herauszustellen.
Ein mögliches Vorgehen kann somit darin bestehen, dass Lernende zunächst einen Zehnerstreifen, anschließend einen Fünferstreifen und letztlich zwei einzelne Plättchen hinzufügen.
Zentral ist dabei, dass die Materialhandlungen nicht nur eigenständig vollzogen, sondern parallel auch möglichst exakt versprachlicht werden. Dies ist vor allem deshalb wichtig, da präzise sprachliche Beschreibungen in den folgenden Phasen des Modells ein notwendiges Element werden. Für obiges Beispiel ist es denkbar, dass Handlung und Notation wie folgt ablaufen:
| Versprachlichung | Materialhandlung |
|---|---|
| „Zuerst lege ich einen Zehnerstreifen in die obere Zeile des Zwanzigerfeldes.“ |
 |
| „Dann lege ich einen Fünferstreifen in die zweite Zeile.“ | |
| „Jetzt ein Plättchen direkt rechts neben den Fünferstreifen.“ | |
| „Dann noch ein Plättchen direkt daneben.“ |
Obiges Procedere kann mit verschiedenen Zahlen vorgenommen werden. Sofern Lernende die darzustellenden Zahlen nicht-zählend am Zwanzigerfeld darstellen und eine gewisse Routine der Abläufe festzustellen ist, kann der Übergang in Phase 2 erfolgen.
Phase 2: Das Kind beschreibt die Materialhandlung mit Sicht auf das Material.
In der zweiten Phase wird die Materialhandlung nicht – wie noch in Phase 1 – vom Lernenden selbst durchgeführt. Zentraler Gegenstand dieser Phase ist es, dass die zuvor durchgeführte Materialhandlung nur noch versprachlicht wird. So ist es die Aufgabe eines Kindes in dieser Phase, einer anderen Person (z. B. einer Förderlehrkraft oder einem Mitschüler bzw. einer Mitschülerin) die durchzuführenden Materialhandlungen zu diktieren. Dabei hat das Kind nicht nur die Aufgabe, zu beschreiben, wie sein Gegenüber handeln soll. Auch ist es die Aufgabe, die Materialhandlungen zu überprüfen, indem selbige aufmerksam beobachtet werden.
Ein möglicher Verlauf dieser Phase – erneut am Beispiel der Zahldarstellung der 17 illustriert – könnte wie folgt aussehen:
| Versprachlichung | Materialhandlung |
|---|---|
| „Lege einen Zehnerstreifen in die obere Zeile des Zwanzigerfeldes.“ |
 |
| „Dann lege einen Fünferstreifen in die zweite Zeile.“ | |
| „Jetzt lege ein Plättchen direkt rechts neben den Fünferstreifen.“ | |
| „Füge nun noch ein Plättchen direkt daneben hinzu.“ |
Erfahrungen zum Einsatz des Vierphasenmodells in Partnerarbeit haben gezeigt, dass dasjenige Kind, welches in dieser Phase die Handlung durchführt, teilweise dazu neigen kann, Handlungen durchzuführen, die es selbst mit dem jeweiligen Arbeitsauftrag verbindet. Die versprachlichten Anweisungen des Partnerkindes fließen nicht immer so ein, wie es sein sollte. In diesem Zusammenhang hat es sich als gewinnbringend herausgestellt, dass die Aufgabe bzw. der Arbeitsauftrag lediglich dem Kind präsentiert wird, welches die Handlungen diktieren soll. Dem handelnden Kind wird selbiger erst nach dem Darstellungsprozess vorgelegt, um eine Überprüfung vorzunehmen. Auf diese Weise kann eine Orientierung der Handlungen mit den Versprachlichungen des Partnerkindes hergestellt werden.
Phase 3: Das Kind beschreibt die Materialhandlung ohne Sicht auf das Material.
Die darauffolgende dritte Phase stimmt strukturell mit der Phase 2 überein. Auch hier ist es die Aufgabe des Lernenden, die in Phase 1 eigenständig durchgeführte Materialhandlung exakt zu diktieren und von einer anderen Person durchführen zu lassen. Jedoch besteht zwischen den Phasen 2 und 3 ein zentraler Unterschied, den es zu beachten gilt: Während in Phase 2 noch die Sicht auf die Materialhandlung des Gegenübers möglich ist, hat das Kind in Phase 3 keine Möglichkeit mehr, die Materialhandlung der zweiten Person direkt zu beobachten. Dies kann entweder durch das Verbinden der Augen erreicht werden oder man stellt einfach einen Sichtschirm zwischen den Kindern auf. Auf diese Weise wird das diktierende Kind angeregt oder gar gezwungen, den Ablauf der Materialhandlung ausschließlich in der Vorstellung nachzuvollziehen. Dadurch gehen die Kinder einen bedeutenden Schritt weg von der konkreten Materialhandlung in Richtung gedanklicher Operationen. Das Kind muss zu jedem Zeitpunkt sowohl die bereits durchgeführten und noch zu vollziehenden Materialhandlungen als auch die jeweils gegenwärtige ikonische Darstellung in der Vorstellung abrufen können.
| Versprachlichung | Materialhandlung |
|---|---|
| „Lege einen Zehnerstreifen in die obere Zeile des Zwanzigerfeldes.“ |
 |
| „Dann lege einen Fünferstreifen in die zweite Zeile.“ | |
| „Jetzt lege ein Plättchen direkt rechts neben den Fünferstreifen.“ | |
| „Füge nun noch ein Plättchen direkt daneben hinzu.“ |
Phase 4: Das Kind arbeitet auf symbolischer Ebene, übt und automatisiert.

Es ist natürlich das Ziel, Kinder von konkreten Handlungen am Material zu lösen. Allerdings sollen sie auch noch in späteren Phasen dazu angeregt werden, diese Materialhandlungen gedanklich zu vollziehen. In diesem Zusammenhang sei darauf hingewiesen, dass das Vierphasenmodell keineswegs als ein Stufenmodell zu verstehen ist. Die Phasen werden also nicht zwingend nacheinander durchgeführt. Für den Fall, dass Kinder bspw. offenkundig Schwierigkeiten in Phase 3 dabei haben, die Materialhandlungen ohne Sicht auf Selbiges exakt zu diktieren, kann eine erneute Durchführung der zweiten Phase hilfreich sein. Genauso kann auch ein Rückschritt von der vierten in die dritte Phase sinnvoll sein. Es darf nicht das primäre Ziel des unterrichtlichen Einsatzes des Vierphasenmodells sein, dieses schnellstmöglich ‚abzuarbeiten’. Wesentlich sollte sein, dass Kinder tragfähige Vorstellungsbilder entwickeln. Manchen Kindern wird dies relativ schnell und ohne Rückschritte in bereits bearbeitete Phasen des Vierphasenmodells gelingen. Andere Kinder werden genau dies benötigen, was ihnen keineswegs verwehrt werden darf:
um am Material zu erklären, etwas darzustellen oder zu argumentieren.“
(Häsel-Weide et al., 2014, S. 114)
Weitere Anwendungsbereiche des Vierphasenmodells
Auf dieser Seite wurde beispielhaft aufgezeigt, wie der Aufbau von Vorstellungen zur nicht-zählenden Zahldarstellung am Zwanzigerfeld anhand des Vierphasenmodells gelingen kann. An dieser Stelle sei jedoch auch auf weitere Möglichkeiten des Vorstellungsaufbaus verwiesen. Auf analoge Weise können weitere Vorstellungen, wie zu verschiedenen Operationen oder Rechenstrategien, aufgebaut werden. So liegt bspw. jeder Rechenstrategie eine konkrete Materialhandlung zu Grunde, die in Phase 1 von den Kindern selbst durchgeführt, in Phase 2 mit Sicht und in Phase 3 ohne Sicht auf das Material diktiert wird, um auf der Grundlage der entwickelten mentalen Bilder Aufgaben auf symbolischer Ebene verständnisbasiert lösen zu können. Auf die Materialhandlungen können die Kinder in der Vorstellung zur Lösung der Aufgaben zurückgreifen.
In diesem Sinne ist das Vierphasenmodell nicht zum Vorstellungsaufbau vereinzelter Aspekte des Mathematiklernens zu verstehen. Es kann als Orientierungsrahmen für einen Mathematikunterricht dienen, der großen Wert auf die Entwicklung mentaler Bilder legt.
- Diagnosegespräche und Fördergespräche
- Diagnoseaufgaben und Förderaufgaben
Auf den Seiten finden Sie unter anderem auch Karten aus der PIKAS-MI-Mathe-Kartei, die sich mit der Darstellung von Zahlen am Zwanzigerfeld sowie am Rechenrahmen befassen. Die Karten finden Sie hier:
|
|
Zahlen mit dem Zwanzigerfeld darstellen |
|
|
Zahlen mit dem Rechenrahmen darstellen |
Zählendes Rechnen ablösen
Die Ablösung vom zählenden Rechnen stellt eine der zentralen Aufgaben im arithmetischen Anfangsunterricht dar. Nicht ohne Grund wird zählendes Rechnen als eines der Hauptsymptome von Rechenschwierigkeiten beschrieben, denn zahlreiche Untersuchungen zeigen, dass die Ablösung vom zählenden Rechnen einem erheblicher Anteil der Schülerinnen und Schüler nicht gelingt. Das gilt nicht nur für den mathematischen Anfangsunterricht. Auch zum Ende der Grundschulzeit lassen sich immer wieder Kinder ausmachen, die noch stark am zählenden Rechnen festhalten. Die Materialien der folgenden Seiten können Sie dabei unterstützen, Kinder bei der Erarbeitung nicht-zählender Rechenstrategien zu unterstützen.
Materialien der Selbstlernplattform PriMakom
Stellenwertverständnis entwickeln
Die Entwicklung eines Stellenwertverständnisses stellt eine wesentliche Herausforderung im Arithmetikunterricht der Grundschule dar. Ein ausgebildetes Stellenwertverständnis ermöglicht, dass Kinder dazu in der Lage sind, flexibel zwischen verschiedenen Darstellungsmodi einer Zahl (z. B. Materialdarstellung, Zahlwort und Zahlzeichen) übersetzen zu können. Hierdurch wird nicht nur die Grundlage dafür geschaffen, dass Zahlen auf unterschiedliche Weise interpretiert werden können. Der Erwerb eines Stellenwertverständnisses stellt auch eine unverzichtbare Grundlage für das Rechnen mit (mehreren) Zahlen dar. Viele Kinder haben jedoch häufig Schwierigkeiten dabei, ein Stellenwertverständnis zu entwickeln. Die Materialien der folgenden Seiten können Abhilfe schaffen, um auftretende Lernhürden nehmen zu können.
Materialien der Selbstlernplattform PriMakom
Materialien des Projekts 'Mathe sicher können'
 Die Materialien des Projekts 'Mathe sicher können' stellen aufeinander abgestimmte Diagnose- und Fördermaterialien bereit, um insbesondere Kinder mit Rechenschwierigkeiten bei der Überwindung von Lernhürden zu unterstützen. Die Materialien ermöglichen es, Schwierigkeiten bei der Entwicklung des Stellenwertverständnisses zunächst aufzudecken, um anschließend mit den passenden Materialien fördern zu können. Die entsprechenden Schülermaterialien sowie Begleitinformationen für Lehrkräfte finden Sie hier. Wählen Sie dort den Förderbaustein N1 an.
Die Materialien des Projekts 'Mathe sicher können' stellen aufeinander abgestimmte Diagnose- und Fördermaterialien bereit, um insbesondere Kinder mit Rechenschwierigkeiten bei der Überwindung von Lernhürden zu unterstützen. Die Materialien ermöglichen es, Schwierigkeiten bei der Entwicklung des Stellenwertverständnisses zunächst aufzudecken, um anschließend mit den passenden Materialien fördern zu können. Die entsprechenden Schülermaterialien sowie Begleitinformationen für Lehrkräfte finden Sie hier. Wählen Sie dort den Förderbaustein N1 an.
Operationsverständnis aufbauen
Der Aufbau tragfähiger Vorstellungen zu den Grundrechenarten Addition, Subtraktion, Multiplikation und Division ist ein wesentlicher Baustein, damit Kinder bei der Überwindung von Rechenschwierigkeiten unterstützt werden können. Ohne die Fähigkeit, den mathematischen Symbolen +, -, • und : Bedeutungen zuschreiben zu können, werden Kinder tiefgehende Schwierigkeiten bei der Bewältigung von Mathematikaufgaben im Verlauf ihrer Grundschulzeit haben. Die folgenden Materialien können Lernende dabei unterstützen, Operationsvorstellungen aufzubauen.
Materialien der Selbstlernplattform PriMakom
Hier finden Sie die Seite sowie die Materialien.
Materialien des Projekts 'Mathe sicher können'
 Die Materialien des Projekts 'Mathe sicher können' stellen aufeinander abgestimmte Diagnose- und Fördermaterialien bereit, um insbesondere Kinder mit Rechenschwierigkeiten bei der Überwindung von Lernhürden zu unterstützen. Die Materialien ermöglichen es, Schwierigkeiten der Kinder hinsichtlich ihrer Operationsvorstellungen zu den vier Grundrechenarten zunächst aufzudecken, um anschließend mit den passenden Materialien fördern zu können. Die entsprechenden Schülermaterialien sowie Begleitinformationen für Lehrkräfte finden Sie hier. Wählen Sie dort die Förderbausteine N3 und N4 an.
Die Materialien des Projekts 'Mathe sicher können' stellen aufeinander abgestimmte Diagnose- und Fördermaterialien bereit, um insbesondere Kinder mit Rechenschwierigkeiten bei der Überwindung von Lernhürden zu unterstützen. Die Materialien ermöglichen es, Schwierigkeiten der Kinder hinsichtlich ihrer Operationsvorstellungen zu den vier Grundrechenarten zunächst aufzudecken, um anschließend mit den passenden Materialien fördern zu können. Die entsprechenden Schülermaterialien sowie Begleitinformationen für Lehrkräfte finden Sie hier. Wählen Sie dort die Förderbausteine N3 und N4 an.
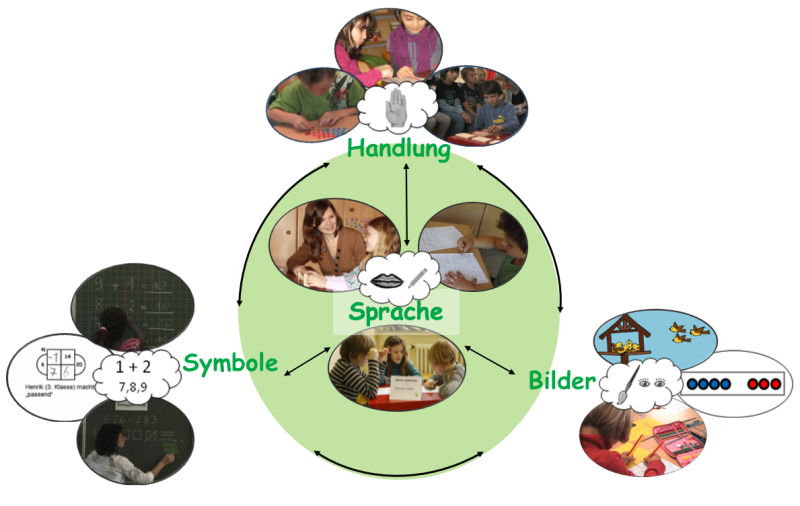
Guter Umgang mit Darstellungsmitteln
„Seit Jahrhunderten ist man sich in der Mathematikdidaktik einig, dass Kinder günstigerweise durch Handlungen lernen" (Lorenz 2011, S. 39).
Im Laufe der vergangenen Jahrhunderte wurden verschiedene Darstellungsmittel erfunden, mit deren Hilfe mathematische Strukturen veranschaulicht werden sollen. Die Bilder, die mit einem Darstellungsmittel (didaktischem Material) erzeugt werden, soll ein Kind verinnerlichen, damit sie später zum Rechnen im Kopf abrufbar sind.
Von „flexiblem Rechnen" spricht man dann, wenn ein Kind im Kopf und ohne Darstellungsmittel, sondern lediglich durch die in der Vorstellung entstandenen Bilder, rechnen kann.
Wie sehen aber solche Handlungen genau aus? Worauf sollte im Mathematikunterricht geachtet werden, damit jedes Kind die Chance hat am Ende rechnen zu können? Diese Fragen sollen im Folgenden genauer betrachtet werden.
Zum Einfinden in das Thema sind hier zunächst unsere Basisinfos sinnvoll, die Sie als Texte (plus Elternbrief) und Plakate herunterladen können.
In dem Prozess der Aneignung mathematischer Bilder ist es von zentraler Bedeutung, Darstellungswechsel zu forcieren. Erst dadurch wird Mathematik erlebbar. D.h. die Schülerinnen und Schüler sollen immer wieder aufgefordert werden, zwischen verschiedenen Darstellungsformen und -mitteln hin und her zu „übersetzen", damit ein mathematisches Muster z. B. einen lebensweltlichen Bezug und somit einen „Sinn" für die Kinder bekommt.
Hierzu haben wir 2 Übungsformate ausgewählt und aufbereitet, die zum Üben des Darstellungswechsels hilfreich sind und dem Aufbau von Zahl- und Operationsvorstellung dienen:
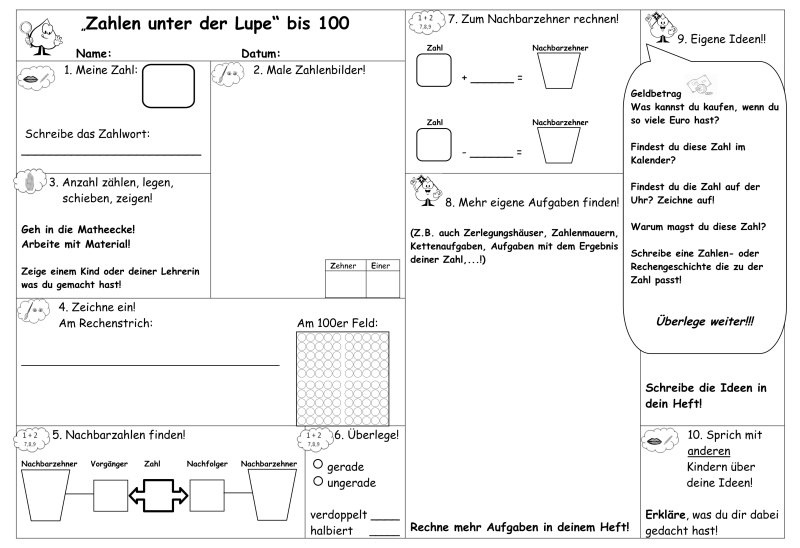
1. Die „Zahlen unter der Lupe"
2. Das „Malquartett"
Außerdem haben wir für Sie einige mathematische Materialien zum Herunterladen vorbereitet. Diese können z. T. als Anschauungsmaterialien für den Unterricht, aber auch für die Hand jedes Kindes – auch zum Üben zu Hause – verwendet werden.
Überdies finden Sie den Text „Unterrichtsanregungen zur Förderung des Darstellungswechsels" mit dazugehörigen Arbeitsblättern.
Basisinfos
Zum Einfinden in das Thema „Guter Umgang mit Darstellungsmitteln" bieten sich die Dokumente der Basisinfos an.
Zahlen unter der Lupe
Lehrer-Material
Schüler-Material
|
|
Arbeitsblatt DIN-A5 – Zahlen unter der Lupe bis 100 | |
|
|
Arbeitsblatt DIN-A4 – Zahlen unter der Lupe bis 100 | |
|
|
|
Weiterführende Forscheraufträge |
Das Malquartett
Lehrer-Material
|
|
Info |
|
|
Malquartett (Demoversion) |
|
|
Wortspeicher |
|
|
Plakat – Wolken groß |
Schüler-Material
|
|
Malquartett 1 |
|
|
Malquartett 2 |
|
|
Malquartett 3 |
Darstellungsmittel
|
|
100er Feld |
|
|
20er Felder |
|
|
Zahlenstrahl 0-100 |
|
|
Zahlenkarten 0-100 |
|
|
Einerkarten mit 10er-Ergänzung |
|
|
Zehnerkarten mit 100er-Ergänzung |
|
|
H_Z_E Material |
|
|
20er Reihen |
Unterrichtsanregungen zur Förderung des Darstellungswechsels
Der Text Unterrichtsanregungen zur Förderung des Darstellungswechels geht auf die Frage ein, warum der Darstellungswechsel im Mathematikunterricht thematisiert und explizit gefördert werden sollte. Außerdem zeigt er inhaltliche und methodische Aspekte für eine mögliche Umsetzung auf. Es werden Unterrichtsanregungen zur Förderung des Darstellungswechsels am Beispiel der Multiplikation gegeben, zu denen Sie ausgewählte Arbeitsblätter herunterladen können.
Weiterführende Informationen
 |
Hier finden Sie das gesamte Material dieser Seite (51,9 MB). |