Funktionen von Sprache

Im täglichen Mathematikunterricht kommt es nicht selten vor, dass Grundschulkinder versuchen, eine Entdeckung oder einen Rechenweg zu beschreiben und dann daran scheitern, ihre Überlegungen verständlich zu formulieren. Über Mathematik zu kommunizieren stellt für sehr viele Grundschulkinder eine nicht zu unterschätzende Herausforderung dar, denn schließlich sind die fach- und bildungssprachlichen Kompetenzen dieser jungen Lernenden oftmals noch nicht ausreichend entwickelt, um sich mathematisch verständlich auszudrücken.

Aber was versteht man nun unter einem sprachbewussten Mathematikunterricht? Und welche Sprachmittel sollten im Mathematikunterricht thematisiert werden? Im Folgenden führen wir diese Fragestellungen näher aus.

Sprache erfüllt im Mathematikunterricht im Wesentlichen zwei zentrale Funktionen:

• In der kommunikativen Funktion dient Sprache der Verständigung, d. h. können Kinder ihre Überlegungen nicht in Worte fassen, so können sie ihre mathematischen Kompetenzen nicht zeigen. Zeitgleich erleichtert eine gemeinsame Sprache das wechselseitige Verständnis.

• Die kognitive Funktion von Sprache beim Mathematiklernen ist oftmals nicht direkt beobachtbar, aber dennoch sehr zentral. Da mathematische Inhalte oft abstrakt sind, brauchen die Kinder eine „Denksprache“, die verdeutlicht, wie z. B. die konkrete Aufgabe „gedacht“ werden kann.

Die beiden Funktionen von Sprache lassen sich in den folgenden Kinderaussagen wiederfinden:

Bekommen die Kinder nur Sprachmittel an die Hand, die die kommunikative Funktion von Sprache ansprechen, so besteht die Gefahr, dass die Kinder Sätze und Wörter auswendig lernen, aber im Grunde nicht verstehen, was genau damit gemeint ist. So ist es kein Hexenwerk, mit immer gleichartigen Sätzen das Muster in schönen Päckchen zu beschreiben. Ob die Kinder sie aber auch denken und damit auch wirklich erklären können, bleibt dann unklar bzw. müsste erfragt werden.

Denkmoment

Überlegen Sie einmal selbst: Wie könnten die oben aufgeführten Versprachlichungen verändert werden, um stärker auf die kognitive Funktion von Sprache schließen zu können?

Zur Auflösung

Die kognitive Funktion von Sprache adressiert somit vor allem die konkreten Darstellungen mit den anschaulichen Materialien. Sie liefert Antworten auf die Frage: Wie würdest du das Muster, die Aufgabe, deinen Rechenweg usw. mit Material legen oder zeichnen?

Es ist nachweislich für Kinder sehr lernförderlich, wenn so oft wie möglich die kognitive Funktion von Sprache im Mathematikunterricht adressiert und passend dazu mit Material gelegt wird. So lernen Kinder im Mathematikunterricht erfolgreich.

 

Kognitive und kommunikative Funktion von Sprache unterstützen durch Kurzaktivitäten

Einige Kurzaktivitäten aus der PIKAS-Mathekartei ermöglichen, dass Sie beide Funktionen von Sprache nicht nur ritualisiert, sondern auch spielerisch im täglichen Unterricht ansprechen können. Sie schulen also sowohl Kommunikations- als auch sprachliche Denkmittel gleichermaßen.

Dies betrifft z. B. folgende Kurzaktivitäten:

• Zahl unter dem Tuch (Nr. 25)
• Finde den Fehler (Nr. 40)

Denkmoment

Schauen Sie sich diese beiden Kurzaktivitäten an und überlegen Sie, wie diese im Mathematikunterricht eingesetzt werden können, sodass sie die kommunikative und kognitive Funktion von Sprache ansprechen.

Zur Auflösung: Zahl unter dem Tuch

Kommunikative Funktion:

• Wenn Sie als Lehrperson die Übung durchführt, müssen die Kinder Sprachmittel wie z. B. Zehnerstange, Einerwürfel, ich lege dazu, ich nehme weg usw. verstehen.
• Wenn die Kinder die Übung durchführen, müssen sie diese Sprachmittel selbst nutzen.

Kognitive Funktion:

• Die Kinder werden gefordert, sich die gelegten Zahlen selbst vorzustellen. Vorstellungsbilder werden damit aktiviert.
• Die Kinder sollten nicht nur die Lösungszahl nennen, sondern ihren Lösungsweg verbalisieren: „Wir hatten 4 Einer, 8 Einer kamen dazu. 10 Einer werden zu einem Zehner. Die Zahl ist 12.” So kann z. B. die Bündelung durch die Verbalisierung verdeutlicht und vertieft werden.

Zur Auflösung: Finde den Fehler

Kommunikative Funktion:

• Wenn Sie als Lehrperson die Übung durchführt, müssen die Kinder Sprachmittel wie z. B. Zehnerstange, Einerwürfel, ich lege dazu, ich nehme weg usw. verstehen.
• Wenn die Kinder die Übung durchführen, müssen sie diese Sprachmittel selbst nutzen.

Kognitive Funktion:

• Die Kinder werden gefordert, sich die gelegten Zahlen selbst vorzustellen. Vorstellungsbilder werden damit aktiviert.
• Die Kinder sollten nicht nur die Lösungszahl nennen, sondern ihren Lösungsweg verbalisieren: „Wir hatten 4 Einer, 8 Einer kamen dazu. 10 Einer werden zu einem Zehner. Die Zahl ist 12.” So kann z. B. die Bündelung durch die Verbalisierung verdeutlicht und vertieft werden.

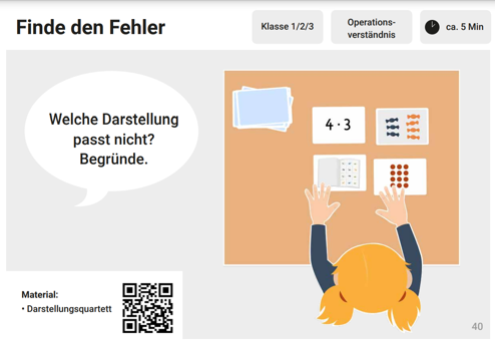
Kognitive und kommunikative Funktion von Sprache unterstützen durch Sprachspeicher 

Eine weitere Unterstützungsmöglichkeit stellen Sprachspeicher – oft auch Wortspeicher genannt – dar. Ein Sprachspeicher ist eine Sammlung von wichtigen Fachausdrücken und Sprachmitteln zum jeweiligen Unterrichtsinhalt (Götze, 2015). Wie er aufgebaut werden kann, wird im Folgenden an einem beispielhaften Sprachspeicher zu schönen Päckchen der Addition illustriert.

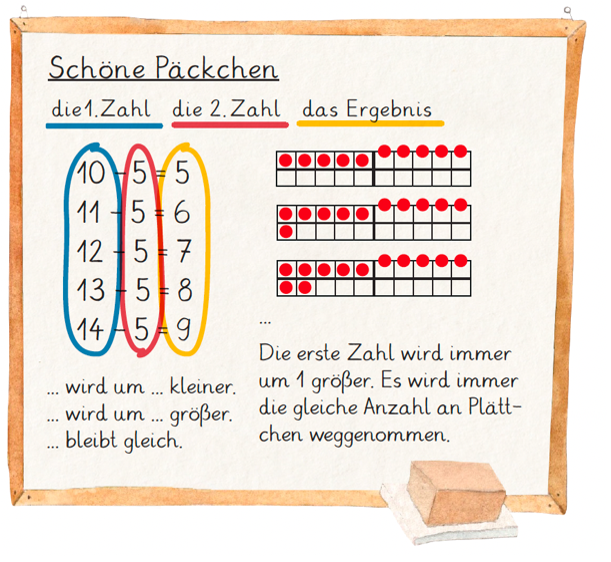
Ein Sprachspeicher, der die Kinder beim Beschreiben und Erklären der Muster in den schönen Päckchen zur Addition unterstützen soll, bietet Ausdrücke an, die helfen, das Muster in den schönen Päckchen zu beschreiben. Diese werden an einem konkreten schönen Päckchen visualisiert, damit die Kinder für sie wichtige Ausdrücke im Sprachspeicher schnell (wieder-)finden können (die erste Zahl, die zweite Zahl, das Ergebnis). Zudem werden zentrale Satzbaustein im Sprachspeicher festgehalten (… wird um ... kleiner.). Die Fachausdrücke und Satzbausteine berücksichtigen die kommunikative Funktion von Sprache. Ebenfalls sind Mittel zum Forschen eingebunden, sodass die Kinder an dem exemplarischen Beispiel die Verbindung der Mittel zum Forschen und der Versprachlichung direkt erkennen und nutzen können (ggf. expliziert durch „Schreibe zu jeder Farbe einen Satz.“). Der linke Teil des Sprachspeichers unterstützt die Kinder somit beim selbstständigen Formulieren eigener Beschreibungen, aber auch beim Nachvollziehen von Beschreibungen anderer. Das Wahrnehmen und Beschreiben des Musters ist aber natürlich nur der erste Schritt. Die Beschreibungen erklären das Muster aber noch nicht (siehe auch Modul 3, Kinder beim Beschreiben und Begründen unterstützen).

Daher werden auf der rechten Seite des Sprachspeichers die Sprachmittel und Visualisierungen aufgeführt, die die kognitive Funktion ansprechen. Damit erhalten die Kinder Angebote, wie sie das Muster sprachlich begründen und am Material zeigen können.

Die Herausforderung an die Kinder besteht nun darin, die vielfältigen Angebot des Sprachspeichers auf weitere schöne Päckchen mit anderen Mustern zu übertragen.

Wenn Sie noch mehr über Sprachspeicher und Forschermittel erfahren möchten, schauen Sie sich doch die folgenden Videos an.

Erklärvideo Sprachspeicher

 

Erklärvideo Mittel zum Forschen

 

Verweise auf weitere Informationen und Materialien zum Thema

Ergänzendes Material auf PIKAS

Mathekartei

Anregungen für Aktivitäten zur Förderung ausgewählter inhaltsbezogener Kompetenzen finden Sie in der Mathekartei

Mittel zum Forschen und co.

Anregungen für den Einsatz von Mitteln zum Forschen und weiteren Unterstützungsmaßnahmen finden Sie im Bereich Fortbildung - Forschermittel und co

Hintergrundwissen in den Partnerprojekten

Weiterführenden Informationen zur Vertiefung finden Sie auch auf folgenden Partnerprojektseiten:

Mahiko Wie Kinder lernen

Allgemeine Informationen zu einem verstehensorientierten Mathematiklernen