Das erwartet Sie in diesem Mini-Modul:
-
Warum ist es wichtig, dass Lernende Zahldarstellungen vernetzen können?
-
Was bedeutet es, Zahldarstellungen zu vernetzen?
-
Welche Aussagen stimmen? Welche Zahldarstellung passt nicht? (Eigenaktivität)
Warum ist es wichtig, dass Lernende Zahldarstellungen vernetzen können?
Für die Ausbildung eines tragfähigen Zahlverständnisses ist das Vernetzen verschiedener Darstellungsformen von Zahlen essenziell. Zahlen sind beides – konkret in unserer Umwelt, z. B. drei Luftballons, und abstrakt, z. B. die Zahl 2 im Mathematikunterricht. Für Kinder ist die Vorstellung von Zahlen deswegen schwierig erfassbar. Nur durch den Aufbau mentaler Vorstellungsbilder können Kinder ein tragfähiges Zahlverständnis ausbilden, das sie später auch für ein fundiertes Stellenwert- oder Operationsverständnis oder auch für die Ausführung von Rechenoperationen benötigen. Schon im Anfangsunterricht sollte deshalb kontinuierlich eine flexible Darstellungsvernetzung angesprochen und letztlich erlernt werden, nicht zuletzt, um Vorstellungsbilder immer wieder zu aktivieren.
Was bedeutet es, Zahldarstellungen zu vernetzen?
Um den Aufbau von Grundvorstellungen zu unterstützen und tragfähig zu fundieren, werden im Mathematikunterricht verschiedene Darstellungen verwendet. Unterschieden werden
-
Handlungen am Material (enaktiv)
-
bildliche Darstellungen (ikonisch)
-
mathematisch-symbolische Darstellungen (symbolisch)
-
sprachliche Darstellungen (verbal).
In der Abbildung werden jeweils Darstellungen zur Zahl 4 gezeigt. Wesentlich ist, dass mit all diesen Darstellungen die gleiche Zahl abgebildet wird.
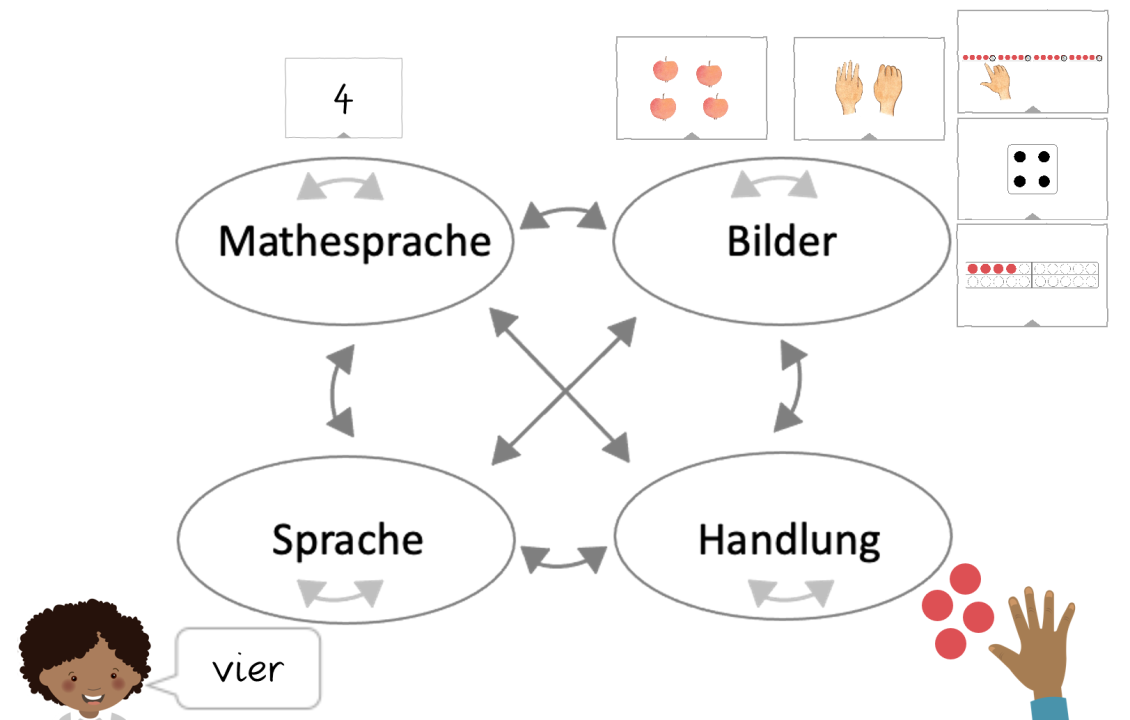
Die Herausforderung besteht nun darin, die einzelnen Darstellungen nicht nebeneinander stehen zu lassen, sondern sie miteinander zu vernetzen. Dabei wird unterschieden zwischen der intermodalen Darstellungsvernetzung, also zwischen den einzelnen Darstellungsarten (sprich: 4 als Würfel oder vier als Wort) und der intramodalen Darstellungsvernetzung, also innerhalb einer Darstellungsart, z. B. 4 als Fingerbild und das vierte Plättchen in der Zahlenkette. Bei einem tragfähigen Vorstellungsaufbau findet eine Verknüpfung zwischen diesen Darstellungsformen statt.
Das kann beispielsweise durch das gemeinsame Sprechen über Zusammenhänge zwischen den Zahldarstellungen gelingen. So sollten Schüler:innen entdecken, was alles "vier" ist, ihre Entdeckungen begründen, aber auch selbst Zahldarstellungen entwickeln und interpretieren. Dies ist eine Voraussetzung für den Erwerb des Zahlbegriffs (vgl. Hasemann & Gasteiger 2014, S. 96). Durch die Darstellungsvernetzung wird letztlich der Aufbau der kardinalen und ordinalen Grundvorstellungen unterstützt (siehe Modul "Grundvorstellungen").
Eigenaktivität: Welche Aussagen stimmen? Welche Zahldarstellung passt nicht?
Weiterführende Informationen aus Partnerprojekten
Weiterführende Informationen zur Vertiefung sowie Material zum Einsatz im Unterricht finden Sie auch auf folgenden Partnerprojektseiten:
Zahlen darstellen
Informationen und Material zum Thema Zahlen darstellen im Unterricht.
Mathe inklusiv
Hintergrundwissen zum Darstellungswechsel und zur Darstellungsvernetzung. Thematisierung der vier Darstellungsformen sowie Unterrichtsanregungen zur Förderung des Darstellungswechsels.
Zahlen darstellen - Übungen
Zahlen darstellen - Lernvideos
Thematisierung der vier Darstellungsformen und der Relevanz sowie Schwierigkeiten von Zahldarstellungen. Vertiefende Übungen und Lernvideos zum Thema.