Das erwartet Sie in diesem Modul
-
Warum ist es wichtig, dass informative Aufgaben im Mathematikunterricht eingesetzt werden?
-
Welche Typen von informativen Aufgaben gibt es?
-
Wie lassen sich Aufgaben informativer gestalten? (Eigenaktivität)
Warum ist es wichtig, dass informative Aufgaben im Mathematikunterricht eingesetzt werden?
Um jedes Kind individuell zu fördern, wird im Mathematikunterricht eine kontinuierliche, prozessorientierte, individuumsbezogene und kompetenzorientierte Art der Leistungsfeststellung angestrebt. In Arithmetik 1/2 wurden dazu verschiedene Diagnoseinstrumente (Modul 1.1) vorgestellt. Sie sollen Einblicke in die mathematischen Denkwege der Kinder ermöglichen. Um damit tatsächlich Informationen über Lösungswege der Lernenden generieren zu können, bedarf es jedoch einer sorgfältigen Aufgabenauswahl.
Es wird zwischen produktorientierten und informativen Aufgaben unterschieden:
Rein produktorientierte Aufgaben geben lediglich Auskunft über das "richtig" / "falsch" einer Aufgabenbearbeitung. Ein Einblick in die Denkwege der Kinder ist kaum möglich. Bei fehlerhaften Lösungen kann nicht festgestellt werden, ob eine Fehlvorstellung vorliegt oder der Fehler "nur" auf mangelnde Konzentration zurückzuführen ist.
Informative Aufgaben geben mehr und detailliertere Informationen über die Lösungswege der Kinder. Diese Informationen bilden die Grundlage für weitere Fördermaßnahmen auf dem individuellen Lernstand jedes Kindes.
Welche Typen von informativen Aufgaben gibt es?
Aufgaben, die für sich alleinstehend keinen hohen Informationsgehalt haben, können mithilfe kleiner Änderungen informativer werden. Es wird zwischen vier Idealtypen informativer Aufgaben unterschieden:
Aufgabenvariationen
Die Veränderung der Darstellung oder Situation kann bei der gleichen Grundaufgabe zu veränderten Vorgehensweisen führen. So kann es sein, dass ein Kind eine Aufgabe in manchen Kontexten lösen kann, in anderen Zusammenhängen aber nicht.
Beispiel: Löst das Kind die Aufgabe 12:3 rein symbolisch anders als im Kontext einer Bild-Sach-Aufgabe?
Nebenrechnungen
Es ist ratsam genügend Platz für Nebenrechnungen und Notizen zu lassen. Diese geben zusätzlich zu den Ergebnissen Einsichten in genutzte Rechenwege. Dadurch können Fähigkeiten sowie Fehlvorstellungen der Kinder besser erkannt werden.
Beispiel: Das Kind nutzt schriftliche und halbschriftliche Rechenverfahren zur Lösung der Aufgabe.
Vorgehensweisen darstellen
Bei geeigneten Aufgaben können mündliche oder schriftliche Beschreibungen der Vorgehensweise eingefordert werden. Selbst wenn Erklärungen nicht mit dem tatsächlichen Vorgehen übereinstimmen, können häufig interessante Einblicke in Denkwege des Kindes gewonnen werden.
Beispiel: Die Erklärung gibt Auskunft über die Nutzung von Aufgabenbeziehungen und das Stellenwertverständnis.
Zusammenhängende Aufgaben
Zusammenhängende Aufgaben sind besonders gut geeignet, um gezielt Fehlermuster festzustellen. Die Aufgaben werden anhand bestimmter Kriterien ausgewählt, beispielsweise anhand aufgabentypischer Schwierigkeitsmerkmale oder der Verwandtschaft von Aufgaben.
Beispiel: Je drei Aufgaben hängen zusammen. Es zeigt sich, dass das Kind wiederholt bei Multiplikationsaufgaben dividiert.
Aufgaben, die eine Darstellungsvernetzung fordern, sind besonders geeignet, um einen Einblick in die Vorstellungen der Kinder zu erhalten. Sie lassen individuelle Zugänge der Schüler:innen zu und machen Fehlvorstellungen frühzeitig sichtbar. Für ein tragfähiges Zahl- und Operationsverständnis müssen Kinder innerhalb einer Darstellungsform und zwischen den verschiedenen Darstellungsformen übersetzen können. Aufgabenvariationen bieten sich durch die Veränderung des Kontextes an, um diese Kompetenzen abzufragen.
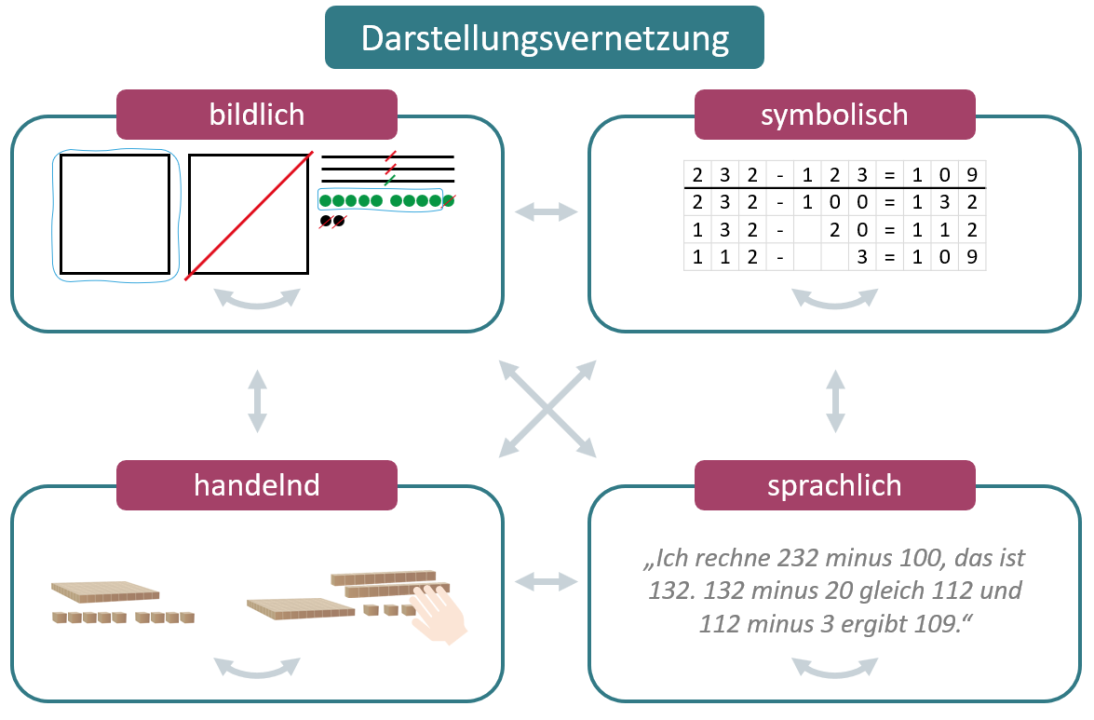Beispielaufgabe: „Rechne die Aufgabe 232-186 halbschriftlich. Lege sie mit Würfelmaterial und notiere dazu das Zahlbild. Erkläre deinen Rechenweg."
Eigenaktivität: Wie lassen sich Aufgaben informativer gestalten?
Weiterführende Informationen aus Partnerprojekten
Weiterführende Informationen zur Vertiefung so wie Material zum Einsatz im Unterricht finden Sie auch auf folgenden Partnerprojektseiten:
Lernstände wahrnehmen
Video Standortbestimmungen
Informationen und Material zu informativen Aufgaben, Standortbestimmungen, Mathebriefkästen, Lerntexten und Beobachtungsbögen.
Standortbestimmungen
Leistungen feststellen
Einsatz von Standortbestimmungen, Diagnose mithilfe des Mathebriefkastens und die Kriterien informativer Aufgaben.
Informative Aufgaben
Diagnostische Gespräche
Thematisierung der Eigenschaften informativer Aufgaben sowie der Vorbereitung, Durchführung und Auswertung diagnostischer Gespräche.
