Das erwartet Sie in diesem Mini-Modul:
-
Warum ist es wichtig, dass Analogien zwischen den Stellenwerten genutzt werden?
-
Was bedeutet es Analogien zwischen den Stellenwerten zu nutzen?
-
Welche Analogieaufgaben gehören zusammen? (Eigenaktivität)
-
Wie können die Analogien versprachlicht werden? (Eigenaktivität)
Warum ist es wichtig, dass Analogien zwischen den Stellenwerten genutzt werden?
Vorgehen wie der "Nullentrick" sollen den Umgang mit großen Zahlen zwar vereinfachen, sind aber nicht anschlussfähig. Dies führt zu Problemen, wenn der Trick auf Aufgaben übertragen wird, bei denen er nicht funktioniert. Die Einführung ist außerdem enorm zeitintensiv. Er funktioniert bei allen vier Rechenoperationen unterschiedlich, die Verfahren müssen jeweils einzeln eingeführt und geübt werden. Es kann schnell passieren, dass ein Vorgehen fälschlicherweise auf eine andere Rechenoperation übertragen wird. Dieses Problem wird dadurch verstärkt, dass die Einführung nicht verständnisbasiert stattfindet, sondern lediglich auf Auswendiglernen basiert.
Im Gegensatz dazu kann das Entdecken und Nutzen von Analogieaufgaben, besonders mithilfe von Material und sprachlich begleitet, verständnisbasiert erfolgen. Die Vorgehensweise ist außerdem anschlussfähig. Sie basiert auf dem Aufbau unseres dekadischen Systems (siehe Arithmetik 1/2: Grundvorstellungen) und lässt sich auf verschiedene Operationen, Zahlenräume, Brüche, Dezimalzahlen und sogar andere Stellenwertsysteme übertragen. Beim Rechnen in großen Zahlenräumen stellt die Nutzung von Analogien eine verlässliche und verständnisbasierte Alternative zum schriftlichen Rechnen dar. Der Fokus auf einzelne Stellenwerte begünstigt eine sichere und effiziente Aufgabenlösung.
Was bedeutet es Analogien zwischen den Stellenwerten zu nutzen?
Stelleneinspluseins und Stelleneinsminuseins
Das Stelleneinspluseins und das Stelleneinsminuseins bilden sich aus vervielfachten Aufgaben des kleinen Einspluseins und -minuseins.
Stelleneinspluseins
Die Summanden einer Aufgabe des kleinen Einspluseins werden mit 10, 100, 1.000, 10.000 oder 100.000 multipliziert.
Beispiel: Aus der Aufgabe 6+8=14 wird die Aufgabe 60.000+80.000=140.000, indem beide Summanden sowie das Ergebnis mit 10.000 multipliziert werden.
Stelleneinsminuseins
Minuend und Subtrahend werden mit 10, 100, 1.000, 10.000 oder 100.000 multipliziert.
Beispiel: Aus der Aufgabe 9-5=4 wird die Aufgabe 90.000-50.000=40.000, indem Minuend und Subtrahend sowie das Ergebnis mit 10.000 multipliziert werden.
Die Summanden bzw. der Minuend und Subtrahend müssen dabei nicht zwingend um denselben Faktor vervielfacht werden.
Eigenaktivität 1: Welche Analogieaufgaben gehören zusammen?
Stelleneinmaleins und Stelleneinsdurcheins
Das Stelleneinmaleins und das Stelleneinsdurcheins bilden sich aus vervielfachten Aufgaben des kleinen Einmaleins und -durcheins.
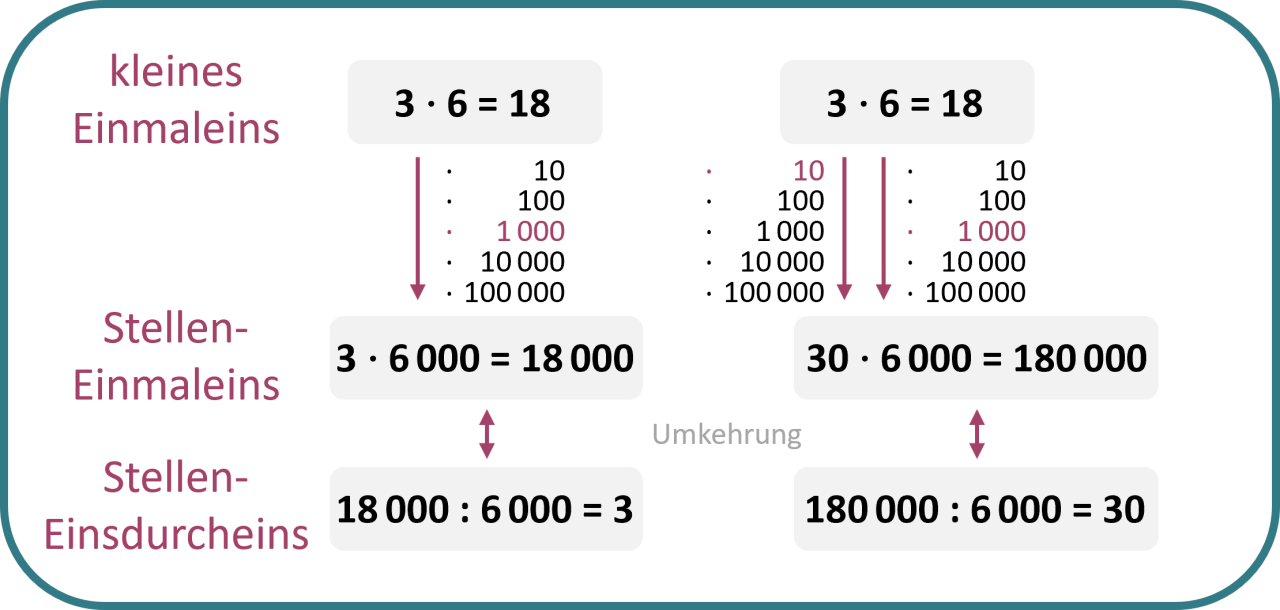
Stelleneinmaleins und -durcheins
Einer oder beide Faktoren werden mit 10, 100, 1.000, 10.000 oder 100.000 multipliziert. Das Stelleneinsdurcheins umfasst die Umkehraufgaben des Stelleneinmaleins.
Beispiel: Aus der Aufgabe 3⋅6=18 werden folgende Aufgaben:
-
3⋅6.000=18.000 (2. Faktor sowie das Ergebnis werden mit 1.000 multipliziert); Umkehraufgabe: 18.000:6000=3
-
30⋅6.000=180.000 (1. Faktor wird mit 10, 2. Faktor mit 1.000, das Ergebnis mit 10 und 1.000 multipliziert); Umkehraufgabe: 180.000:6000
Eigenaktivität 2: Wie können die Analogien versprachlicht werden?
Weiterführende Informationen aus Partnerprojekten
Weiterführende Informationen zur Vertiefung sowie Material zum Einsatz im Unterricht finden Sie auch auf folgenden Partnerprojektseiten:
Standortbestimmungen mit Handreichungen zu Kopfrechnenaufgaben des Zehnereinpluseins, Zehnereinsminuseins und Zehnereinmaleins im Tausenderraum sowie dem Stelleneinpluseins, Stelleneinmaleins und -durcheins im Millionenraum.
Thematisierung der Grundlagen des Zehnereinspluseins und -minuseins und des Zehnereinmaleins und -durcheins im Tausenderraum sowie des Stelleneinspluseins und -minuseins und des Stelleneinmaleins und -durcheins im Millionenraum. Vertiefende Übungen und Lernvideos zum Thema.