Das erwartet Sie in diesem Mini-Modul:
-
Warum ist es wichtig, dass Lernende halbschriftlich multiplizieren können?
-
Wie kann die halbschriftliche Multiplikation im Unterricht erarbeitet werden?
-
Welche Strategien nutzen die Lernenden und wie stellen sie diese dar und beschreiben sie? (Eigenaktivität)
Warum ist es wichtig, dass Lernende halbschriftlich multiplizieren können?
Das halbschriftliche Rechnen legt im Hunderterraum die Basis für das Kopfrechnen. Die Notation der Rechenschritte sollte Schritt für Schritt so weit reduziert werden, dass Aufgaben flexibel im Kopf berechnet werden können. Aufgaben in größeren Zahlenräumen können jedoch nicht so leicht ohne Notation im Kopf gelöst werden, sodass die halbschriftlichen Rechenstrategien hier Rechnungen z. B. im Tausenderraum erst möglich machen (vgl. Padberg & Benz 2011, S. 173). Zudem unterstützen sie das Erlernen eines verständnisbasierten Rechnens und tragen nicht nur zum reinen Ausführen von Verfahren bei. Dies schafft die Voraussetzung für das schriftliche Rechnen und die Algebra.
Die halbschriftlichen Rechenstrategien der Multiplikation werden auf der Grundlage der ausgebildeten Multiplikationsvorstellungen und des kleinen Einmaleins sowie des Zehnereinmaleins entwickelt und auf den Tausenderraum angewendet.
Wie kann die halbschriftliche Multiplikation im Unterricht erarbeitet werden?
Zu den Hauptstrategien der halbschriftlichen Multiplikation zählen das stellenweise Rechnen mit dem Malkreuz, das schrittweise Rechnen, die Ableitungsstrategien Hilfsaufgabe und Vereinfachen sowie Mischformen dieser. Ziel des Unterrichts ist es, dass die Schüler:innen die verschiedenen Strategien kennenlernen und verstehen und möglichst geschickt zum Lösen einer Aufgabe einsetzen. Die Wahl einer Strategie hängt von der jeweiligen Malaufgabe und der eigenen Vorliebe ab.
Im folgenden Video werden die gängigsten Hauptstrategien erläutert und Unterstützungsmöglichkeiten der Lernenden vorgestellt.
Hinweis: Das vorliegende Material ist urheberrechtlich geschützt. Es ist nicht erlaubt, Videos oder Fotos dieser Website herunterzuladen, zu vervielfältigen oder weiterzuverbreiten.
Die schnelle Strategie des Vereinfachens eignet sich nur für wenige Aufgaben und benötigt einen guten Zahl- und Aufgabenblick (vgl. Padberg & Benz 2011, S. 188). Die Ausgangsaufgabe wird mithilfe des Konstanzgesetzes in eine leichtere Aufgabe umgewandelt. Dabei erfolgt eine gegensinnige Veränderung der beiden Faktoren um den gleichen Wert, indem:
-
ein Faktor mit dem Wert multipliziert
-
und der andere Faktor durch den Wert dividiert wird.
Auf diese Weise verändert sich das Ergebnis der Aufgabe nicht. Die Konstanz des Produktes kann anschaulich mit Punktestreifen dargestellt werden.
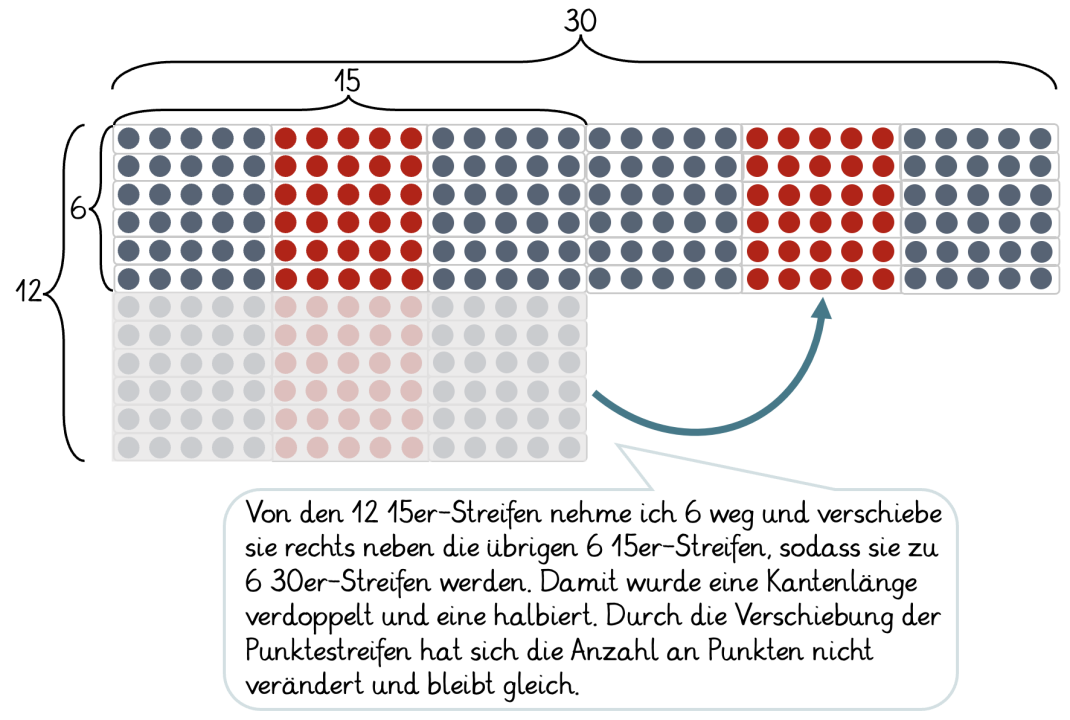
Die genannten Strategien können auch als Mischformen auftreten. Eine weitere Möglichkeit besteht darin, dass die Kinder einzelne Rechenschritte nur im Kopf berechnen und nicht aufschreiben.
 Mischform aus schritt- und stellenweisem Rechnen
Mischform aus schritt- und stellenweisem Rechnen
Eigenaktivität: Welche Strategien nutzen die Lernenden und wie stellen sie diese dar und beschreiben sie?
Weiterführende Informationen aus Partnerprojekten
Weiterführende Informationen zur Vertiefung sowie Material zum Einsatz im Unterricht finden Sie auch auf folgenden Partnerprojektseiten:
Zahlenrechnen
Durchführung vertiefender Aktivitäten zu den halbschriftlichen Rechenstrategien aller Grundrechenarten mit besonderem Fokus auf Diagnose und Förderung.
Thematisierung der halbschriftlichen Rechenstrategien in den verschiedenen Grundrechenarten sowie möglicher Schwierigkeiten und Darstellung eines Aufgabenformats zum halbschriftlichen Rechnen.
Grundlagenwissen sowie Übungen und Lernvideos für Schüler:innen zur halbschriftlichen Multiplikation im Tausenderraum- sowie die Nutzung des Stelleneinmaleins im Millionenraum.
Mathe sicher können
Förderbausteine N6 A "Ich kann sicher mit Stufenzahlen multiplizieren und dividieren" und N6 B "Ich kann sicher multiplizieren und meine Rechenwege erklären".