2.2. Darstellungsvernetzung und Aufgabenbeziehungen

Das erwartet Sie in diesem Mini-Modul:

Warum ist es wichtig, dass Lernende Darstellungen vernetzen und Aufgabenbeziehungen nutzen?
Was bedeutet es Darstellungen zu vernetzen und Aufgabenbeziehungen zu nutzen?
Welche Darstellungsform liegt vor? (Eigenaktivität)

Warum ist es wichtig, dass Lernende Darstellungen vernetzen und Aufgabenbeziehungen nutzen?

Das Verständnis des Stellenwertsystems und der sichere Umgang mit Zehnern und Einern sind die Basis für die Orientierung im erweiterten Zahlenraum. Kinder sollten das dezimale Bündelungsprinzip deshalb bereits im Hunderterraum verinnerlichen. Ein tragfähiges Stellenwertverständnis zeichnet sich insbesondere dadurch aus, dass Kind erklären kann, wie:

die Ziffern des Zahlenzeichens ("5" und "4"),
die Bestandteile des Zahlwortes (vierundfünfzig)
und die Anzahlen der einzelnen Bündelungseinheiten zusammenhängen (5 Zehner, 4 Einer).

Die Fünf steht links von der Vier, weil es fünf Zehner sind. Die Zahl heißt Vierundfünfzig, weil sie aus vier Einern und fünf Zehnern (also fünfzig) zusammengesetzt ist (vgl. Schulz, 2014, S. 150). Um diese Einsichten zu erlangen, müssen Lernende verschiedene Darstellungsformen zueinander in Verbindung setzen und mentale Vorstellungsbilder zu Stellenwerten aufbauen.

Was bedeutet es Darstellungen zu vernetzen und Aufgabenbeziehungen zu nutzen?

Um den Aufbau des Stellenwertverständnisses zu unterstützen, werden im Mathematikunterricht verschiedene Darstellungen verwendet:

mathematisch-symbolische Darstellungen (symbolisch)
bildliche Darstellungen (ikonisch)
sprachliche Darstellungen (verbal)
Handlungen am Material (enaktiv)

Die folgende Abbildung zeigt beispielhaft verschiedene Darstellungen zur Zahl 32.

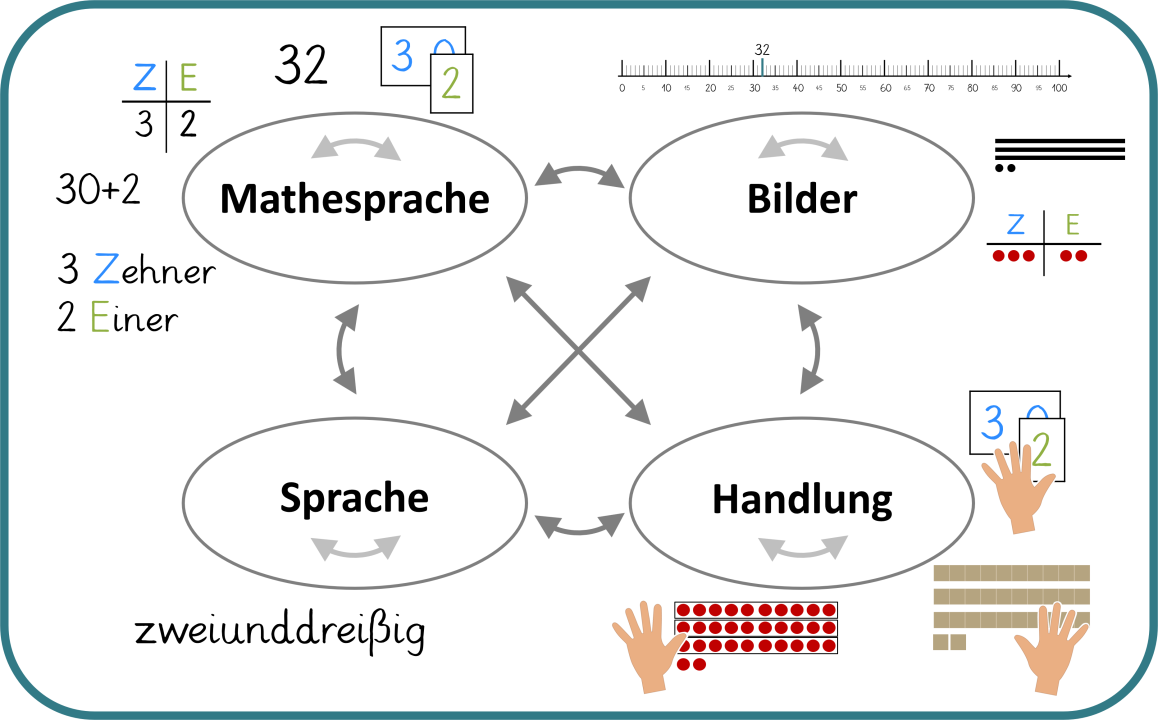
Wichtig ist, dass die einzelnen Darstellungen nicht bloß nebeneinander stehen, sondern vernetzt werden. Diese Darstellungsvernetzung erfolgt auf zwei Arten:

intermodal: zwischen verschiedenen Darstellungsebenen (z. B. die gesprochene Zahl "zweiunddreißig" und die mit Würfelmaterial gelegte Zahl)
intramodal: innerhalb einer Darstellungsebene (z. B. die symbolisch notierte Zahl "32" sowie die Zahl "32" in der Stellentafel)

Einige Anschauungsmaterialien sind besonders geeignet, um Lernenden Strukturen des dezimalen Stellenwertsystems zugänglich zu machen:

2.2 Anschauungsmaterialien Stellenwertverständnis

Weitere Informationen zu Anschauungsmaterialen sowie zur Anschlussfähigkeit auch über das 2. Schuljahr hinaus, finden Sie in Modul "Anschauungsmaterial".

Die Schreib- und Sprechweise in der deutschen Sprache kann eine besondere Schwierigkeiten auf dem Weg zu einem sicheren Stellenwertverständnis darstellen:

Inverse Sprechweise: Bei den meisten Zahlwörtern weicht die Sprechweise von der Notation der Zahlen ab (z. B. gesprochen: vier-und-fünfzig, aber 54 geschrieben)
Unregelmäßige Bildung: Einige Zahlen werden unregelmäßig gebildet (z. B. elf, zwölf, drei-zehn, vier-zehn)

Um Schwierigkeiten bei der Bildung von Zahlworten und der Notation von Zahlen zu begegnen, sollten Lernende daher materialgestützt und sprachlich unterstützt Einsicht in das das dekadische Stellenwertsystem entwickeln.

Das Bild zeigt einen beispielhaften Wortspeicher zur Unterstützung des "Zahlen Sprechens" aus der Praxiserprobung.

Eigenaktivität: Welche Darstellungsform liegt vor?

2.2 Eigenaktivität

Weiterführende Informationen aus Partnerprojekten

Weiterführende Informationen zur Vertiefung sowie Material zum Einsatz im Unterricht finden Sie auch auf folgenden Partnerprojektseiten:

Mathe inklusiv

Diagnose und Förderung: Basisaufgabe "Zahlen darstellen" mit Fokus auf dem Darstellungswechsel. Reduktion und Erweiterung der Basisaufgabe

Stellenwertverständnis

Thematisierung der Grundlagen des dezimalen Stellenwertsystems, Bündeln und Entbündeln und der Umgang mit ungewohnten Darstellungen im Stellenwertsystem anhand von Schüler:innendokumenten und Eigenaktivitäten

Zehner und Einer

Thematisierung der Grundvorstellungen des Stellenwertverständnisses im Zahlenraum bis 100. Vertiefende Übungen und Lernvideos zum zum Bündeln und Entbündeln, Hören, Lesen und Sprechen von Zahlen sowie dem Rechnen mit Zehnern.