Das erwartet Sie in diesem Mini-Modul:
-
Warum ist es wichtig, dass Lernende halbschriftlich subtrahieren können?
-
Wie kann die halbschriftliche Subtraktion im Unterricht erarbeitet werden?
-
Welche Strategien nutzen die Lernenden und wie stellen sie diese dar und beschreiben sie? (Eigenaktivität)
Warum ist es wichtig, dass Lernende halbschriftlich subtrahieren können?
Während sich z. B. Aufgaben mit einem einstelligen Subtrahenden oder glatten Zehner- bzw. Hunderterzahlen im Tausenderraum gut im Kopf berechnen lassen, ist bei komplizierteren Aufgaben das Nutzen halbschriftlicher Rechenstrategien nötig. Diese ermöglichen ein vorteilhafteres Rechnen durch das Zerlegen oder Verändern einer Aufgabe und fördern sowohl das flexible Rechnen als auch das Entwickeln individueller Lösungswege.
Die halbschriftlichen Rechenstrategien der Subtraktion wurden bereits im Hunderterraum mit den Schüler:innen im Unterricht erarbeitet (siehe Arithmetik 1/2: Halbschriftliche Strategien). Daher kann an das erworbene Wissen angeknüpft und dieses auf den Tausenderraum angewendet werden. Es wird die Grundlage für das schriftliche Rechnen und die Algebra geschaffen.
Wie kann die halbschriftliche Subtraktion im Unterricht erarbeitet werden?
Zu den Hauptstrategien der halbschriftlichen Subtraktion zählen das stellenweise und schrittweise Rechnen, das Ergänzen, die Ableitungsstrategien Hilfsaufgabe und Vereinfachen sowie Mischformen dieser. Ziel des Unterrichts ist es, dass die Schüler:innen die verschiedenen Strategien kennenlernen und verstehen und möglichst geschickt zum Lösen einer Aufgabe einsetzen.
Im folgenden Video werden die gängigsten Hauptstrategien erläutert. Zudem wird auf mögliche Schwierigkeiten aufmerksam gemacht und Unterstützungsmöglichkeiten der Lernenden vorgestellt.
Hinweis: Das vorliegende Material ist urheberrechtlich geschützt. Es ist nicht erlaubt, Videos oder Fotos dieser Website herunterzuladen, zu vervielfältigen oder weiterzuverbreiten.
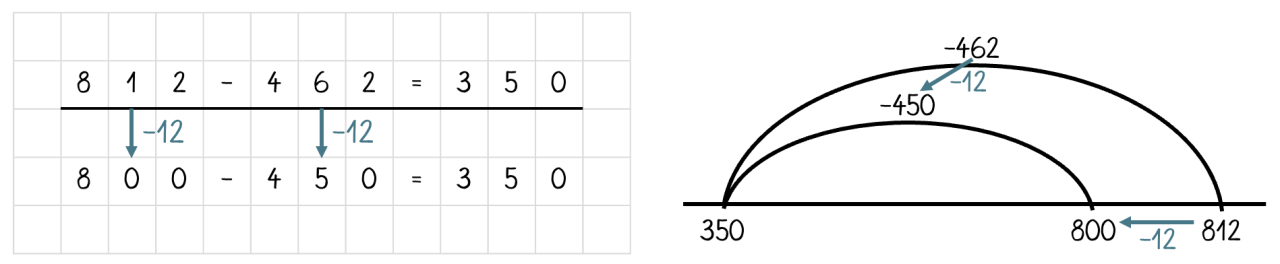
Eine weitere geschickte, aber zugleich komplexe Strategie ist das Vereinfachen. Hier stehen wie bei der Hilfsaufgabe die operativen Beziehungen im Vordergrund. Die Ausgangsaufgabe wird aus einer einfacheren Aufgabe abgeleitet. Dabei findet das Konstanzgesetz der Differenz Anwendung, indem eine gleichsinnige Veränderung von Minuend und Subtrahend erfolgt (vgl. Padberg & Benz 2011, S. 182). Somit ist kein weiterer Schritt zur Korrektur notwendig. Das Ergebnis der Aufgabe bleibt trotz der Veränderung gleich. Zur Erleichterung des Verständnisses kann die gleichsinnige Veränderung am Würfelmaterial erarbeitet werden.
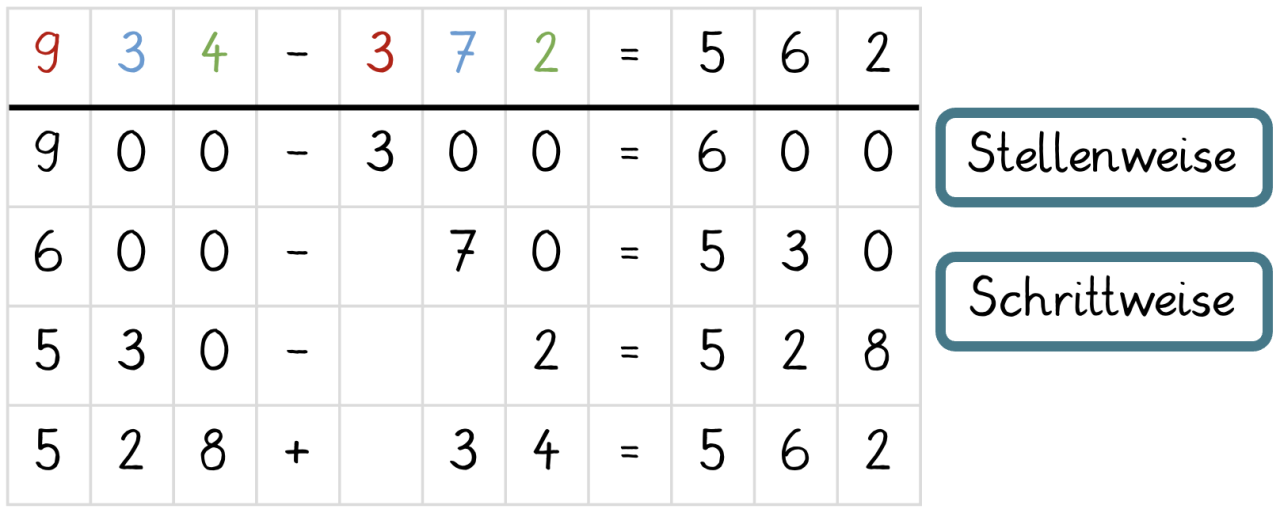
Die Kinder nutzen auch Mischformen der genannten Strategien. Bei der Mischform aus stellen- und schrittweisem Rechnen erfolgt sowohl eine Zerlegung des Minuenden als auch Subtrahenden in ihre Stellenwerte. Zunächst werden stellenweise die Hunderter miteinander verrechnet. Anschließend wird schrittweise verfahren.
Eigenaktivität: Welche Strategien nutzen die Lernenden und wie stellen sie diese dar und beschreiben sie?
Weiterführende Informationen aus Partnerprojekten
Weiterführende Informationen zur Vertiefung sowie Material zum Einsatz im Unterricht finden Sie auch auf folgenden Partnerprojektseiten:
Lernen auf eigenen Wegen - Addieren und Subtrahieren auf eigenen Wegen
Informationen und Material zur Erarbeitung der halbschriftlichen Subtraktion im Unterricht.
primakom
Informationen und Unterstützungsmaßnahmen zu den halbschriftlichen Rechenstrategien am Beispiel der Subtraktion im Tausenderraum.
Thematisierung der halbschriftlichen Rechenstrategien in den verschiedenen Grundrechenarten sowie möglicher Schwierigkeiten und Darstellung eines Aufgabenformats zum halbschriftlichen Rechnen.
Mathe sicher können
Zahlenrechnen - Förderbaustein N5 A Rechenwege Addition und Subtraktion.