Das erwartet Sie in diesem Mini-Modul:
-
Warum ist der Einsatz von produktiven Übungen im Unterricht wichtig?
-
Was wird unter effektivem Üben verstanden und welche produktiven Aufgabenformate gibt es?
-
Zu welchem Zeitpunkt findet effektives Üben statt und wie können Übungsaufgaben aussehen? (Eigenaktivität)
Warum ist der Einsatz von produktiven Übungen im Unterricht wichtig?
Die Integration effektiven Übens in den Mathematikunterricht ist zentral für die Umsetzung eines aktiv-entdeckenden Lernens. Entgegen einer auf Klein- und Gleichschrittigkeit basierenden Unterrichtspraxis fordert das ganzheitlich orientierte, effektive Üben eigene Denkleistungen der Schüler:innen. Mathematiklernen erfolgt durch Einsicht und aktive Sinnstiftung (vgl. Krauthausen 1993, S. 206) und wird als konstruktiver, entdeckender Prozess verstanden. Produktive Aufgabenformate schließen neben dem Training der Rechenfertigkeiten auch prozessbezogene Kompetenzen ein.
Üben ist damit im wesentlichen das Wiederaufnehmen eines (entdeckenden) Lernprozesses, das Nocheinmalnachbilden, Nocheinmalnachbauen von Lernsituationen. An der zunehmenden (und nicht schon gleich vermittelten) Mechanisierung von Verfahren, an der Verflechtung von Wissen sowie an der geläufigeren Handhabung von Strategien werden die Schüler bewußt und aktiv beteiligt. (Winter 1984, S. 10)
Folgende Gründe sprechen für das effektive Üben im Unterricht:
-
Vorhandenes Wissen und Können wird gesichert, vernetzt und vertieft (vgl. MSB NRW 2021, S. 73).
-
Im Sinne einer natürlichen Differenzierung können sich alle Kinder nach ihren Möglichkeiten beteiligen.
-
Die Bewusstheit und Verantwortung für das eigene Lernen werden gefördert und es werden bessere Langzeiterfolge als im kleinschrittigen, reglementierten Unterricht erzielt.
-
Lernen und Üben entsprechen dem Wesen der Mathematik und ihren Anwendungen. So wird eine Motivation aus der Sache heraus ermöglicht und ein natürlicher Rahmen für soziales, sinnerfülltes Lernen geschaffen (vgl. Wittmann 1994, S. 164).
Was wird unter effektivem Üben verstanden und welche produktiven Aufgabenformate gibt es?
Von Üben kann dann gesprochen werden, wenn ein Satz von Wissenselementen bzw. eine Fertigkeit bei einer Serie von gleichartigen Aufgaben wiederholt angewandt wird. Beim effektiven Üben wird ein vielfältiges Angebot von verschiedenartigen Übungsformen bereitgestellt, die inhaltliche und allgemeine Lernziele verzahnen und unterschiedliche Darstellungsformen stärker berücksichtigen.
Im Folgenden werden vier Übungsphasen formuliert, bei denen jeweils unterschiedliche Lernaktivitäten im Vordergrund stehen.
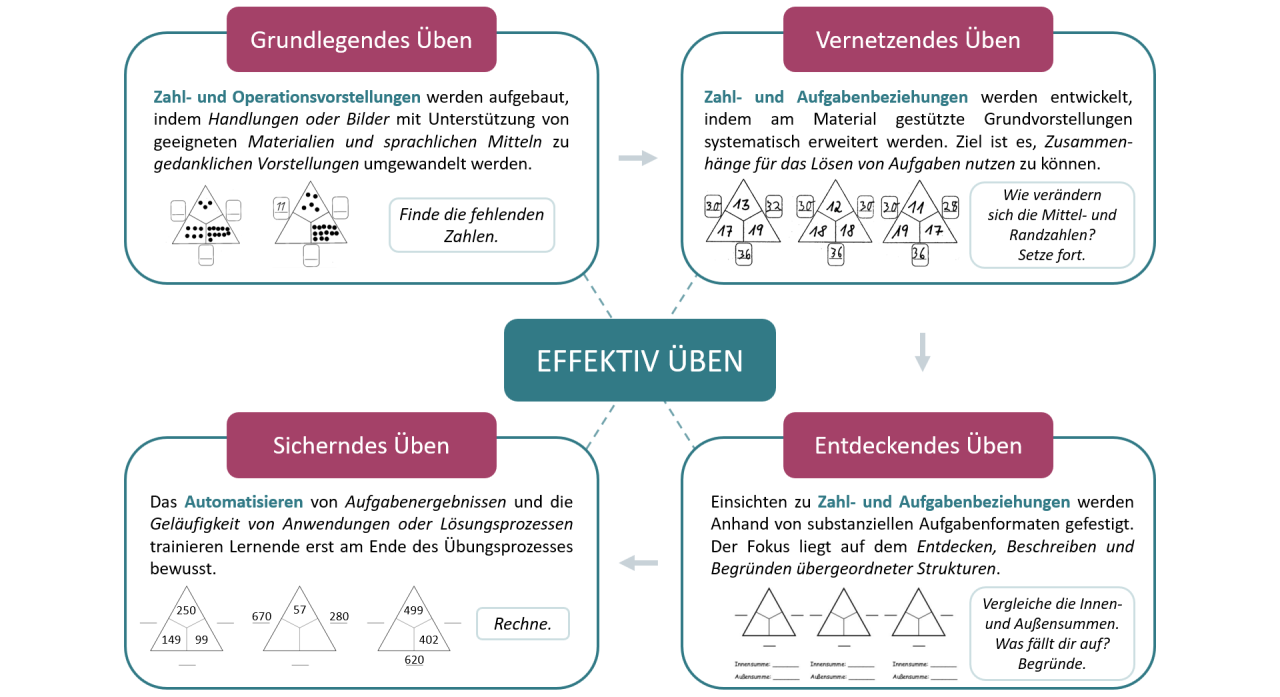
Wir haben hier eine Auswahl an Aufgabenideen zu produktiven Aufgabenformaten zusammengestellt. Diese reichen über gängige Formate bis hin zu neuen spannenden arithmetischen Formaten.
Zu welchem Zeitpunkt findet effektives Üben statt und wie können Übungsaufgaben aussehen?
Weiterführende Informationen aus Partnerprojekten
Weiterführende Informationen zur Vertiefung sowie Material zum Einsatz im Unterricht finden Sie auch auf folgenden Partnerprojektseiten:
Beziehungsreiches Üben
Subtraktion produktiv üben
Informationen und Beispielaufgaben zu verschiedenen Übungstypen allgemein sowie zum produktiven Üben der Subtraktion anhand von Entdeckerpärchen, Stellenwerten und Umkehrzahlen. Vorstellung der Übungsmatrix.
Gestütztes Üben
Informationen zum Übungsprozess und Materialeinsatz.
IRI-Zahlen
Schöne Päckchen
"Triff die 50"
Vorstellung der Aufgabenformate und Erklärung der mathematischen Entdeckungen und Hintergründe.