Das erwartet Sie in diesem Modul:
-
Warum ist das Nutzen von Beziehungen und Strukturen zwischen Divisionsaufgaben wichtig?
-
Was bedeutet es, Beziehungen und Strukturen zwischen Divisionsaufgaben nutzen zu können?
-
Welche Umkehraufgaben sind zu erkennen? (Eigenaktivität)
Warum ist das Nutzen von Beziehungen und Strukturen zwischen Divisionsaufgaben wichtig?
Wie bei den anderen Grundrechenarten wird auch bei der Division zwischen einfachen und schwierigeren Aufgaben unterschieden (Padberg & Benz, 2011, S. 162). Entsprechend ist die Nutzung von Beziehungen zwischen Divisionsaufgaben hilfreich für das geschickte Lösen schwieriger Aufgaben mithilfe von einfacheren "Kernaufgaben". Durch den engen Zusammenhang zwischen Division und Multiplikation können auch Multiplikationsaufgaben zum Lösen von Divisionsaufgaben herangezogen werden. Aus dem Grund sollte die Erarbeitung und Festigung des Multiplikationsverständnisses vorausgegangen sein (Padberg & Benz, 2011, S. 152).
Ein tragfähiges Verständnis von Aufgabenbeziehungen und die Fähigkeit, es zum Lösen schwieriger Divisionsaufgaben einzusetzen, sind im Verlauf des weiteren Mathematikunterrichts von großer Bedeutung, da ein bloßes Auswendiglernen von Aufgaben für das Lösen von Divisionsaufgaben im größeren Zahlenraum nicht ausreicht. Weiterhin wird auf diese Weise die Grundlage für das verständnisbasierte schriftliche Dividieren gelegt.
Was bedeutet es, Beziehungen und Strukturen zwischen Divisionsaufgaben nutzen zu können?
Die Kernaufgaben des kleinen Einsdurcheins haben unterschiedliche Besonderheiten, die ein Verinnerlichen und schnelles Abrufen der Aufgaben erleichtern. Es handelt sich um Aufgaben mit dem...
-
Divisor 1: Dividend und Ergebnis identisch
-
Divisor 2: Ergebnis ist die Hälfte des Dividenden
-
Divisor 5: Umkehraufgaben der Multiplikation (5er-Reihe) häufig leicht zu merken
-
Divisor 10: Ergebnis ist ein Zehntel des Dividenden
und dem...
-
Ergebnis 1: Dividend und Divisor identisch
-
Ergebnis 2: Dividend ist das Doppelte des Divisors
-
Ergebnis 5: Umkehraufgaben der Multiplikation (5er-Reihe) häufig leicht zu merken
-
Ergebnis 10: Dividend ist das Zehnfache des Divisors
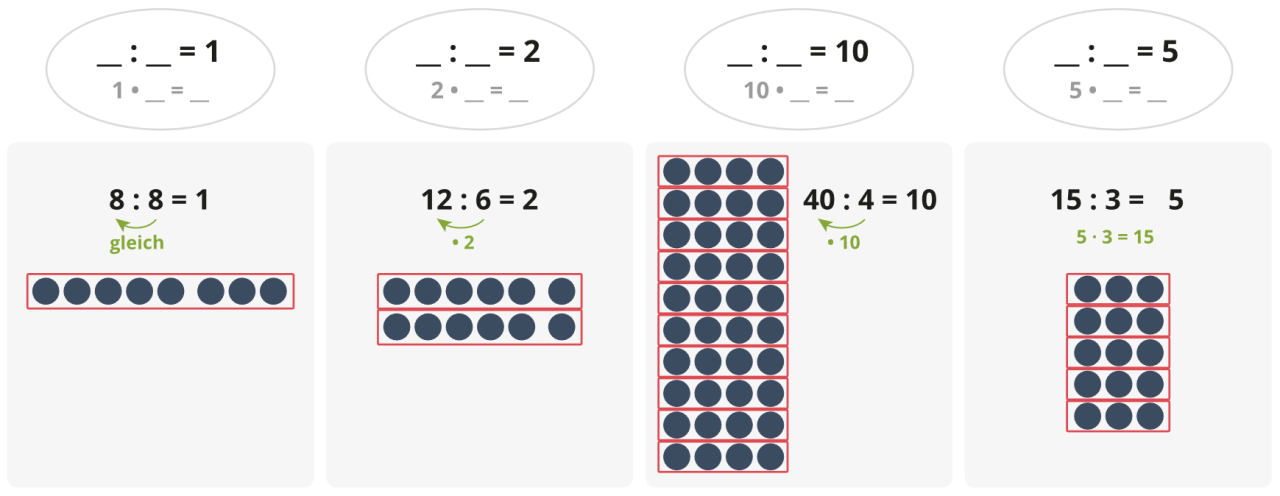
Die Ergebnisse dieser Kernaufgaben sollten Kinder bereits früh auswendig abrufen können. Sie können dann genutzt werden, um sich schwierigere Aufgaben zu erschließen.
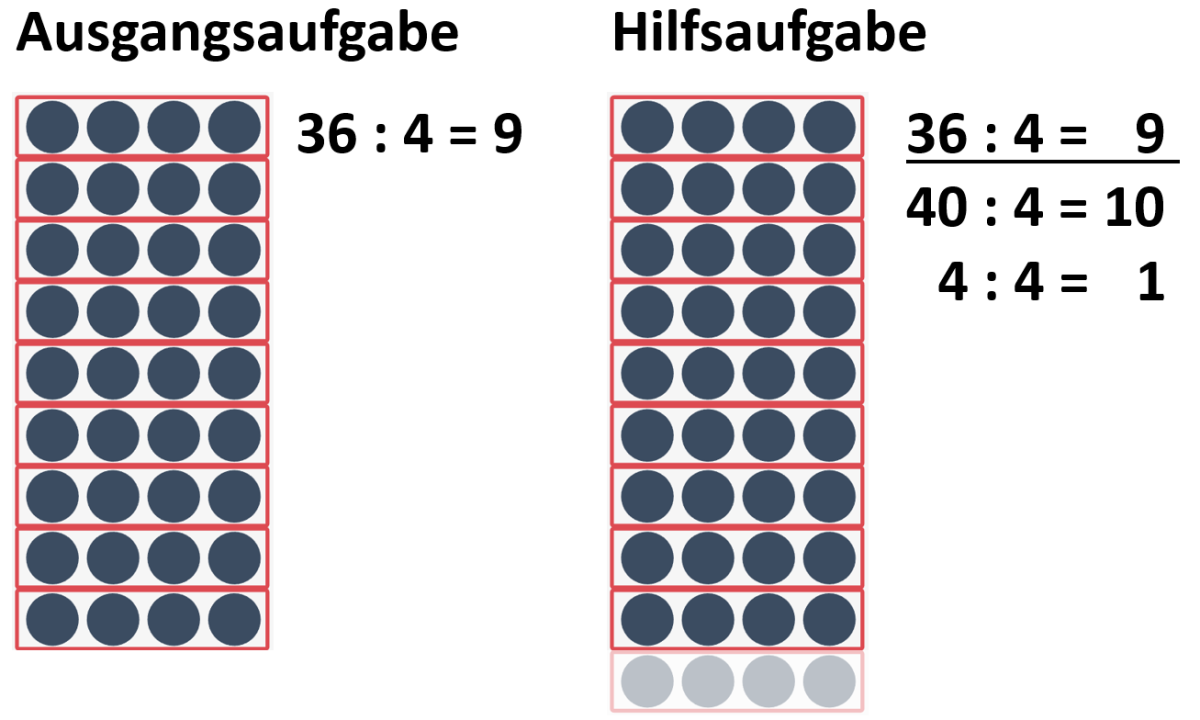
Eine Strategie zum Lösen schwieriger Aufgaben ist das Nutzen von Hilfsaufgaben. Das heißt, der Dividend kann bei einer Divisionsaufgabe so zerlegt werden, dass zwei einfachere Teilaufgaben entstehen. Diese werden dann als „Hilfsaufgaben“ zur Lösung der Ausgangsaufgabe genutzt (Götze, Selter & Zannetin, 2019, S. 84).
Die Aufgabe 36:4 kann beispielsweise mithilfe der Kernaufgaben 40:4 (Aufgabe mit Ergebnis 10) und 4:4 (Aufgabe mit Ergebnis 1) gelöst werden. Vom Ergebnis 10 wird anschließend 1 subtrahiert, da für die Aufgabe 40:4 ein Vierer hinzugenommen wurde.
Zum Zusammenhang zwischen Division und Multiplikation
Für ein ausreichendes Verständnis der Division ist die Erkenntnis, dass die Rechenoperation mit der Multiplikation eng verknüpft ist, zentral.
„Wenn der Zusammenhang zwischen Multiplikation und Division verstanden ist und die Lösungen von Einmaleinsaufgaben als Faktenwissen abgerufen werden können, dann können die Divisionsaufgaben als Umkehrungen der Multiplikationsaufgaben gelöst werden“ (Schipper, Ebeling & Dröge, 2015, S. 116).
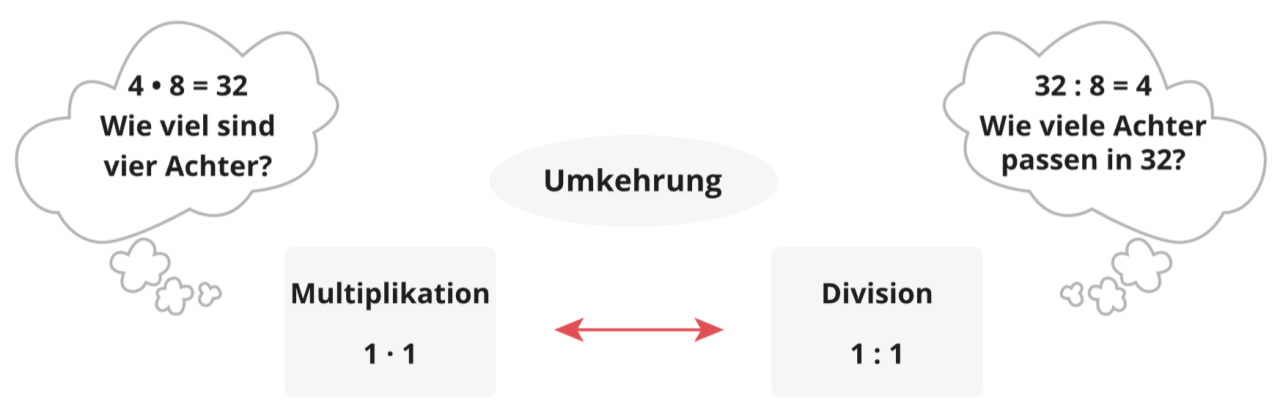
Divisionsaufgaben werden so mithilfe der Frage "Wie oft passt die Zahl x (Divisor) in die Zahl y (Dividend, Gesamtmenge)?" gelöst.
Zum Beispiel ist 4⋅8 = 32 die Umkehraufgabe von 32:8 und die Frage lautet: "Wie viele Achter passen in 32?". Es wird auf das Zahlentripel aus 4, 8 und 32 zurückgegriffen, das bereits aus der Multiplikation bekannt und verinnerlicht ist. Der Zusammenhang zwischen Multiplikation und Division kann beispielsweise an Punktefeldern aufgezeigt werden.
Die Verknüpfung beider Operationen sollte verständnisbasiert und nicht durch reines Auswendiglernen von Regeln erfolgen. Zur Veranschaulichung können Punktefelder oder die Malreihe (siehe Modul 6.1) eingesetzt werden. Die folgenden Beispiele bilden die Umkehrung der Division in verschiedenen Sachkontexten anhand von Handlungen mit Material ab.
Eigenaktivität: Welche Umkehraufgaben sind zu erkennen?
Weiterführende Informationen aus Partnerprojekten
Weiterführende Informationen zur Vertiefung so wie Material zum Einsatz im Unterricht finden Sie auch auf folgenden Partnerprojektseiten:
Division üben
Materialien und Unterrichtsbeispiele zum Kennenlernen und Automatisieren von Kernaufgaben sowie zum Erkennen und Nutzen operativer Zusammenhänge zwischen Divisionsaufgaben.
Sicher im 1:1 - Übungen
Sicher im 1:1 - Lernvideos
Übungen zur verständnisbasierten Automatisierung der Kernaufgaben des 1:1 und Erarbeitung von Strategien zum Lösen weiterer 1:1 - Aufgaben.