5.2 Darstellungsvernetzung Multiplikation

Das erwartet Sie in diesem Modul:

• Warum ist es wichtig, dass Darstellungsformen miteinander vernetzt werden?
• Was bedeutet es, die Darstellungsvernetzung flexibel anwenden zu können?
• Welche Darstellungen passen zur Aufgabe? (Eigenaktivität)

Warum ist es wichtig, dass Darstellungsformen miteinander vernetzt werden?

In Handlungen, Bildern, Sprache und Symbolen bestimmte Rechenoperationen zu erkennen oder darzustellen, erfordert die Fähigkeit zur Darstellungsvernetzung. Entsprechend ist für das Operationsverständnis grundlegend, flexibel zwischen Darstellungen wechseln zu können. Das bedeutet, „zwischen […] verschiedenen ‚Sprachen‘ hin und her übersetzen zu können, also Verbindungen herstellen zu können zwischen konkreten, häufig in Alltagssprache beschriebenen, (Alltags-)Situationen und mathematischen Symbolen und Rechenoperationen“ (Gerster & Schultz, 2004, S. 388).

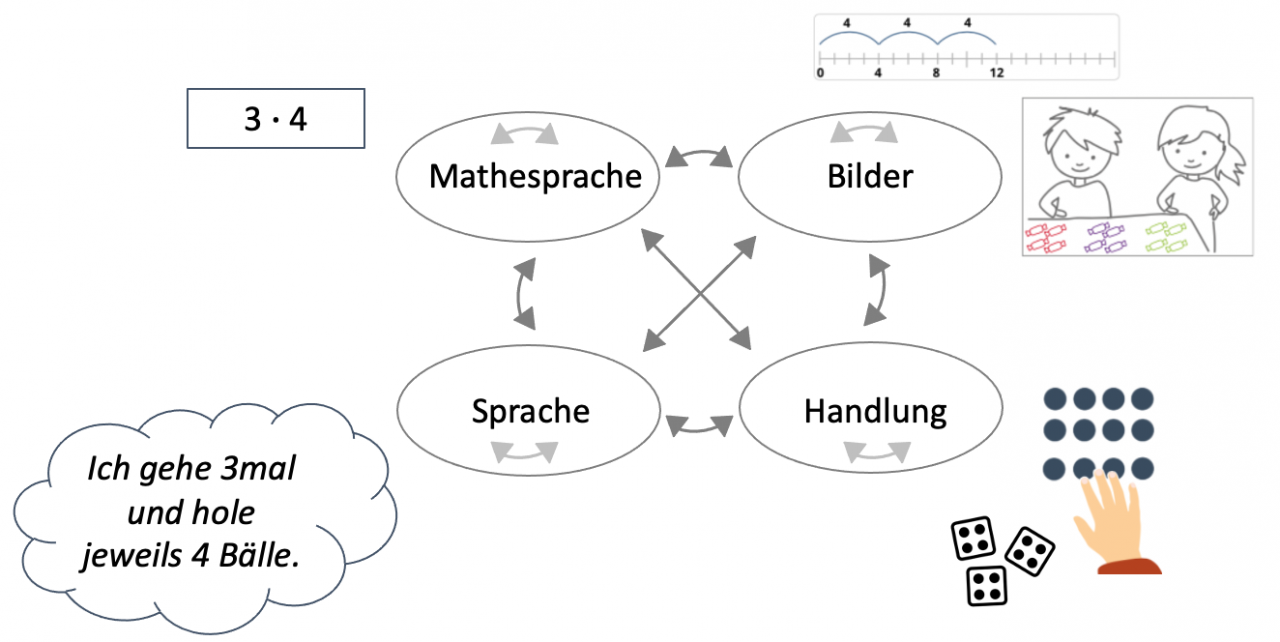
Indem Rechenwege, Ergebnisse und mathematische Strukturen auf verschiedene Weisen dargestellt werden, können Erklärungen und Erkenntnisse entsprechend nachvollziehbar gemacht werden. Unterschiedliche Darstellungen ermöglichen demnach vielfältige Einsichten in die Operationen und Strukturen. So lassen sich auch beispielsweise Rechengesetze, wie das Kommutativ- und Assoziativgesetz, auf kindgerechte Weise an Punktefeldern erläutern, wodurch eine Grundlage für das Verständnis und Funktionieren von Rechenstrategien geschaffen wird. Übersetzungsaktivitäten fördern daher auch die Entwicklung von flexiblem Rechnen.

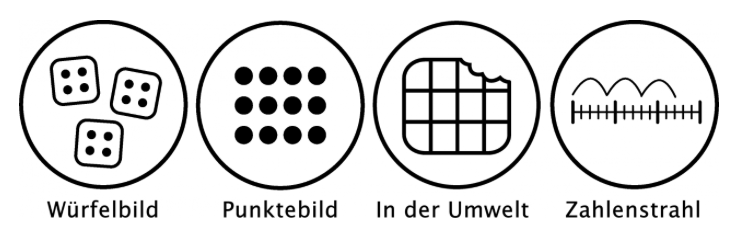
Allgemein wird zwischen Würfelbildern, Punktefeldern, lebenswirklichen Bildern, Rechengeschichten und Zahlenstrahl-Darstellungen übersetzt. Die Multiplikation wird so anhand flächiger, gruppierter und linearer Darstellungen sowie anhand von Sachsituationen in Wort und Bild thematisiert. Die Darstellungsvernetzung im Rahmen von Sachaufgaben verknüpft Mathematik und Alltag und macht die Operationsvorstellungen der Multiplikation für Sachsituationen anwendbar.

Was bedeutet es, die Darstellungsvernetzung flexibel anwenden zu können?

Flexibel zwischen Darstellungen übersetzen zu können bedeutet, auf unterschiedliche Grundvorstellungen zurückgreifen und insbesondere die Übersetzung und Verbindung von verschiedenen Darstellungsformen begründen zu können. Es wird zwischen zwei Arten von Darstellungsvernetzung unterschieden:

Intermodale Darstellungsvernetzung: zwischen den vier Darstellungsformen

Intramodale Darstellungsvernetzung: innerhalb einer Darstellungsform

So wird bei der sogenannten intramodalen Darstellungsvernetzung beispielsweise von einer bildlichen in eine andere bildliche Darstellung gewechselt (vgl. Schulz & Schülke, 2017; Kuhnke, 2013). Wichtig für die Förderung und Entwicklung eines Operationsverständnisses ist also, alle Darstellungsformen im Mathematikunterricht in den Blick zu nehmen und die Passung der Darstellungswechsel begründen zu lassen.

Im Zuge der Thematisierung der Darstellung können auch Schwierigkeiten aufgedeckt werden. Beispielsweise „[fokussieren] Kinder […] bei dem Wechsel von Darstellungen auf bestimmte Relationen, Einzelelemente oder Anzahlen bzw. Ergebnisse, die sie mit den weiteren Darstellungen abgleichen. Sie blenden somit beispielsweise Form, Farbe und teilweise auch die gegebene Anordnung bei bildlichen Darstellungen aus“ (Kuhnke, 2013, S. 265).

Für die Kinder passen zum Beispiel dann zwei Darstellungen gut zusammen, wenn beide Darstellungen dasselbe Ergebnis haben. So ordnet das Kind die Aufgabe 2⋅4 den acht Stickern zu, obwohl diese nicht in zwei Viergruppen angeordnet sind (Kuhnke, 2013, S. 166f.)

Auch können die Kinder einzelne Elemente fokussieren, die in beiden Darstellungen gleichermaßen vorkommen (z. B. einzelne Zahlen oder das Operationszeichen). Beispielsweise werden zwei rote und vier blaue Bonbons als die Faktoren 2 und 4 gedeutet und ein grünes Bonbon als Malzeichen, sodass die Aufgabe 2⋅4 zu der Darstellung passt (Kuhnke, 2013, S. 172). Auch hier wird das Ergebnis sowie die Anzahl und Größe der Gruppen nicht berücksichtigt.

Dieselbe Relation in beiden Darstellungen kann für die Kinder ebenfalls ein Kriterium sein, weshalb die Darstellungen übereinstimmen (z. B. alle Darstellungen, in die sich etwa "drei Vierer" hineindeuten lassen, unabhängig von der eigentlichen Anordnung) (Kuhnke, 2013, S. 265). Zum Beispiel wird ungeachtet der Farben und Anordung der Plättchen die Aufgabe 2⋅4 in der Darstellung erkannt, da nur dieselbe Relation fokussiert wird (ebd., S. 180ff.)

Für ein tragfähiges Multiplikationsverständnis ist es demnach wichtig, neben der Anregung verschiedenster Darstellungsvernetzungen mit den Kindern auch immer wieder darüber ins Gespräch zu kommen, warum eine Darstellung für sie passt, um einseitige Fokussierungen und Fehler beim Darstellungswechsel zu thematisieren und zu vermeiden.

Weiterführende Informationen aus Partnerprojekten

Weiterführende Informationen zur Vertiefung sowie Material zum Einsatz im Unterricht finden Sie auch auf folgenden Partnerprojektseiten:

Malquartett

Multiplikationsaufgaben in verschiedenen Darstellungen erkennen und zuordnen und die Darstellungsvernetzung bei der Multiplikation fördern.

Operationsverständnis Multiplikation

Basisinformationen zum Operationsverständnis und exemplarische Unterrichtsanregungen zu verschiedenen Darstellungsformen der Multiplikation.

Operationen verstehen 

Aufbau und Förderung eines flexiblen Operationsverständnisses mit Unterstützungs- und Diagnosehinweisen für Kinder mit Lernschwierigkeiten.