Das erwartet Sie in diesem Mini-Modul:
-
Warum ist das Nutzen von Beziehungen und Strukturen zwischen Divisionsaufgaben wichtig?
-
Was bedeutet es, Beziehungen und Strukturen zwischen Divisionsaufgaben nutzen zu können?
-
Welche Aufgabenbeziehungen werden genutzt? (Eigenaktivität)
Warum ist das Nutzen von Beziehungen und Strukturen zwischen Divisionsaufgaben wichtig?
Bei der Division wird zwischen sogenannten "Kern- oder Königsaufgaben" und "schwierigeren Aufgaben" unterschieden. Ein flexibles Erkennen und Nutzen von Aufgabenbeziehungen ist hilfreich, um schwierige Aufgaben mithilfe von Kernaufgaben geschickt zu lösen. Durch den engen Zusammenhang zwischen Division und Multiplikation können auch Multiplikationsaufgaben zum Lösen von Divisionsaufgaben herangezogen werden. Aus dem Grund sollte die Erarbeitung und Festigung des Multiplikationsverständnisses vorausgegangen sein (Padberg & Benz, 2011, S. 152).
Ein tragfähiges Verständnis von Aufgabenbeziehungen und die Fähigkeit, es zum Lösen schwieriger Divisionsaufgaben einzusetzen, sind im Verlauf des weiteren Mathematikunterrichts von großer Bedeutung, um:
-
Aufgaben im größeren Zahlenraum zu lösen (Auswendiglernen von Aufgaben ist dann nicht mehr möglich)
-
flexibles und schnelles Kopfrechnen zu fördern,
-
die Grundlage für das verständnisbasierte schriftliche Dividieren zu legen,
-
und algebraische Strukturen anzubahnen.
Was bedeutet es, Beziehungen und Strukturen zwischen Divisionsaufgaben nutzen zu können?
Die Kernaufgaben des kleinen Einsdurcheins weisen bestimmte Muster auf, die ein Verinnerlichen und schnelles Abrufen der Aufgaben erleichtern. Es handelt sich um Aufgaben mit dem...
-
Divisor 1: Dividend und Quotient identisch (8 : 1 = 8)
-
Divisor 2: Quotient ist die Hälfte des Dividenden (12 : 2 = 6)
-
Divisor 5: Umkehraufgaben der Multiplikation (5er-Reihe) häufig leicht zu merken (15 : 5 = 3, weil 5 · 3 = 15)
-
Divisor 10: Quotient ist ein Zehntel des Dividenden (40 : 10 = 4)
und dem...
-
Quotient 1: Dividend und Divisor identisch (8 : 8 = 1)
-
Quotient 2: Dividend ist das Doppelte des Divisors (12 : 6 = 2)
-
Quotient 5: Umkehraufgaben der Multiplikation (5er-Reihe) häufig leicht zu merken (15 : 3 = 5, weil 3 · 5 = 15)
-
Quotient 10: Dividend ist das Zehnfache des Divisors (40 : 4 = 10)
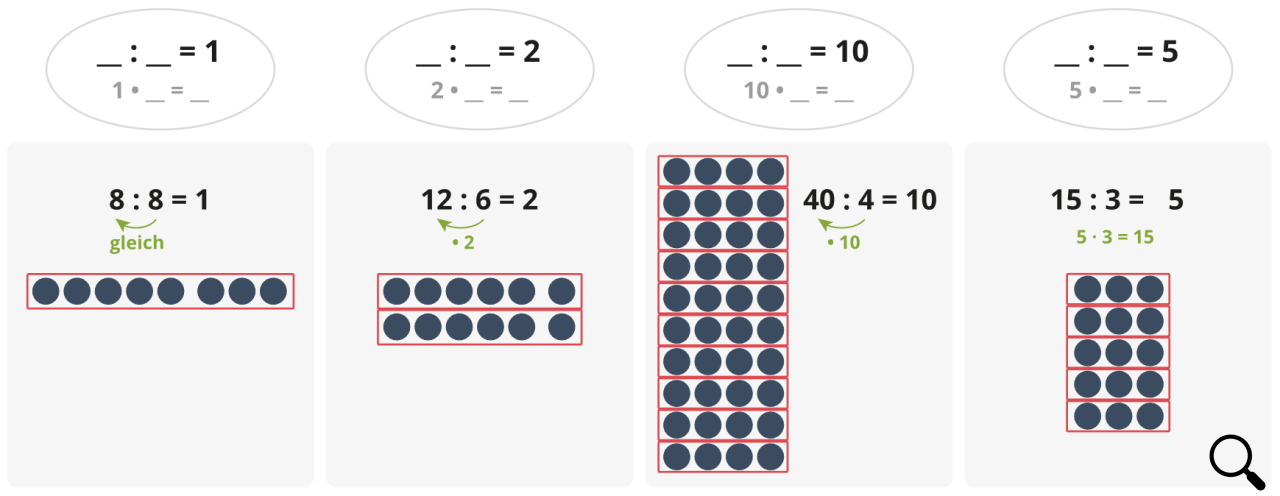
Die Ergebnisse dieser Kernaufgaben sollten Kinder bereits früh auswendig abrufen können. Sie können dann genutzt werden, um sich schwierigere Aufgaben zu erschließen.
Eigenaktivität: Welche Aufgabenbeziehungen werden genutzt?
Weiterführende Informationen aus Partnerprojekten
Weiterführende Informationen zur Vertiefung sowie Material zum Einsatz im Unterricht finden Sie auch auf folgenden Partnerprojektseiten:
Standortbestimmung mit diagnostischen Aufgaben zur geschickten Division (Umkehraufgaben und Nachbaraufgaben)
Materialien und Unterrichtsbeispiele zum Kennenlernen und Automatisieren von Kernaufgaben sowie zum Erkennen und Nutzen operativer Zusammenhänge zwischen Divisionsaufgaben.
Sicher im 1:1 - Übungen
Sicher im 1:1 - Lernvideos
Übungen zur verständnisbasierten Automatisierung der Kernaufgaben des 1:1 und Erarbeitung von Strategien zum Lösen schwieriger Aufgaben.