Zentrale Unterrichtsziele
Das Kind ist in der Lage, ...
-
Zerlegungsbäume zu lösen, d.h. Zahlen multiplikativ zu zerlegen bzw. natürliche Zahlen sicher zu dividieren und somit ihre Teiler zu bestimmen.
-
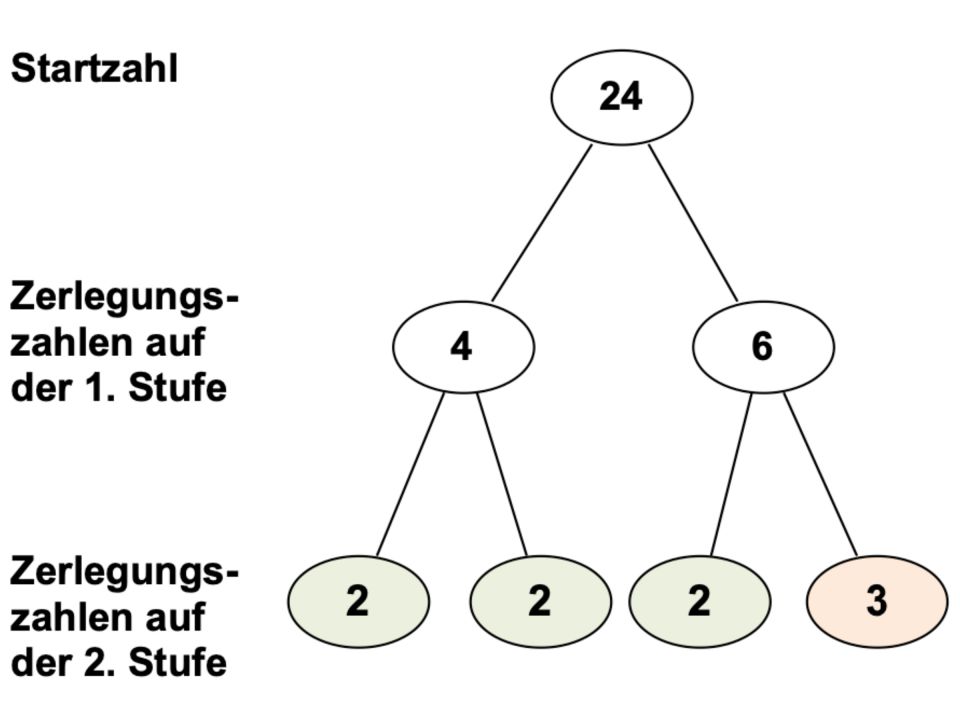
Begriffe zum Thema „Zerlegungsbäume“ (z.B. „Startzahl“, „Zerlegungszahlen“, „Ast“, „1. Stufe“, „2. Stufe“) fachgerecht zu verwenden.
-
die zugrundeliegende Struktur von Zerlegungsbäumen zu beschreiben und zu begründen.
-
zunehmend systematisch alle Zerlegungen zu einer Startzahl aufzuspüren und deren Vollständigkeit zu begründen.
-
Vermutungen zu Zerlegungsbäumen aufzustellen und zu überprüfen.
Zentrale Unterrichtsinhalte
-
Zerlegungsbäume kennenlernen (z.B. mit dem Spiel „Wer zerlegt zuletzt?“)
-
ein Regelplakat zum Konstruktionsprinzip der Zerlegungsbäume erstellen
-
einen Wortspeicher zum Thema „Zerlegungsbäume“ anlegen
-
Zerlegungsbäume mit vorgegebenen Startzahlen berechnen
-
eigene Zerlegungsbäume erfinden
-
Auffälligkeiten an Zerlegungsbäumen entdecken und beschreiben (verbal und/oder mit Hilfe von Forschermitteln)
-
Forscheraufträge zu Zerlegungsbäumen bearbeiten (z.B. „Finde alle Zerlegungsbäume mit der Startzahl 24“)
-
Zerlegungsbäume mit Zahlenlücken vervollständigen
-
strukturierte und unstrukturierte Übungen zu Zerlegungsbäumen durchführen
-
Vermutungen zu Zerlegungsbäumen aufstellen und überprüfen (z.B. bei Zusammenhängen zwischen Startzahlen)
Exemplarisches Unterrichtsmaterial
Schwerpunkte der Unterrichtsaktivitäten: Förderung und Vertiefung des Operationsverständnisses der Division durch das Kennenlernen, Erforschen und Lösen von Zerlegungsbäumen
Klassenstufe: 3-6